Kapitel 9: Grenzwerte (S. 131)

Aufgabe 1

Hier ist eine Skizze zur ersten Orientierung sehr hilfreich.

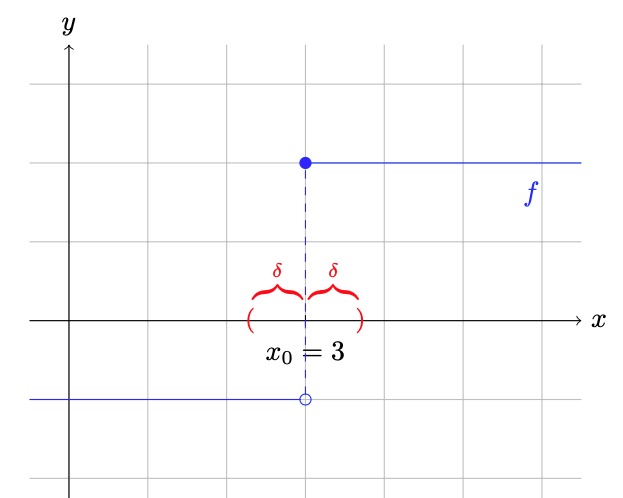
Hätte die Funktion nun an der Stelle \(x_{0}=3\) einen Grenzwert \( a \), so müsste ja insbesondere zu \(\varepsilon=1\) ein Intervall \(\mathrm{I}=(x_{0}-\delta,x_{0}+\delta)\) existieren, so dass für alle Werte \(x\) im Intervall \(\mathrm{I}\) gerade

\(|f(x)-a|<1\)

erfüllt ist. Nun existiert aber (vgl. Skizze), egal wie klein wir das Intervall um die Stelle \(x_{0}=3\) wählen, immer ein \(x_{1}\), das kleiner als \(x_{0}\) ist und auch ein \(x_{2}\), das größer als \(x_{0}\) ist. Gäbe es nun einen Grenzwert \( a\), dürfte dieser also um höchstens eins vom Funktionswert \(f(x_{1})=-1\) abweichen, also

\( -2<a<0 \)

sein. Andererseits dürfte \(a\) auch nur um eins vom Funktionswert \(f(x_{2})=2\) abweichen und damit

\(1<a<2 \)

sein. Beides zugleich ist aber nicht möglich und daher kann ein Grenzwert nicht existieren.

Aufgabe 2

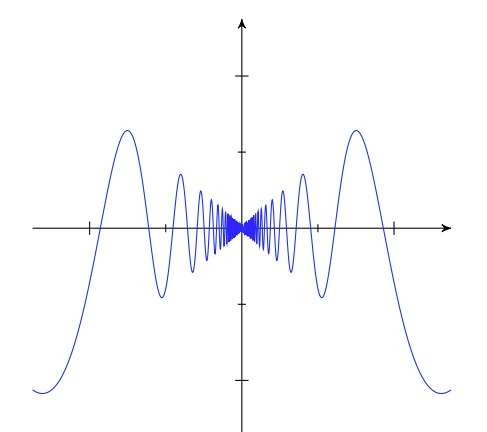
Wir müssen also zu jedem beliebig vorgegebenen \(\varepsilon>0\) ein Intervall \(\mathrm{I}\) um \(x_{0}=0\) angeben in dem alle Funktionswerte um weniger als \(\varepsilon\) vom Grenzwert \(a=0\) abweichen.

Sei also nun ein \(\varepsilon>0\) vorgelegt. Nun ist der Abstand der Funktionswerte zum Grenzwert \(a=0\) ja gerade

\(\displaystyle|f(x)-a|=\left|x\cdot\sin\left(\frac{1}{x}\right)-0\right|=|x|\cdot\left|sin(\left(\frac{1}{x}\right)\right|\)

Da nun (wie im Tipp beschrieben) der Sinus nur Werte zwischen -1 und 1 annimmt, ist

\(\left|\sin\left(\frac{1}{x}\right)\right|<1\)

und damit ist der Abstand der Funktionswerte \(f(x)\) zum Grenzwert immer kleiner als der Abstand der zugehörigen Abszisse \(x\) zur Stelle \(x_{0}=0\), d.h.

\(\displaystyle|f(x)-a|=|x|\cdot\left|sin(\left(\frac{1}{x}\right)\right|<|x|\cdot 1=|x-0|=|x-x_0|\,.\)

Wählen wir also als Intervall zum Beispiel alle \(x\) die näher als \(\varepsilon/2\) an \(x_{0}=0\) liegen, gilt für die zugehörigen Funktionswerte gerade

\(|f(x)-0|<|x-0|<\frac{\varepsilon}{2}<\varepsilon.\)

Ein passendes Intervall ist also

\(\mathrm{I}=\left(x_{0}-\frac{\varepsilon}{2},x_{0}+\frac{\varepsilon}{2}\right)=\left(-\frac{\varepsilon}{2},\frac{\varepsilon}{2}\right)\,.\)

Es gibt aber natürlich noch viel mehr „passende Intervalle“. Zum Beispiel hätten auch die Intervalle \(\mathrm{I}=\left(-\frac{2\varepsilon}{3},\frac{2\varepsilon}{3}\right)\,,\;\mathrm{I}=\left(-\frac{1\varepsilon}{16},\frac{\varepsilon}{16}\right)\) oder \(\mathrm{I}=\left(-\frac{7\varepsilon}{15},\frac{7\varepsilon}{15}\right)\) funktioniert. Nach unseren Überlegungen ist nur entscheidend, dass der Abstand, den die Elemente in diesen Intervallen zu \(x_{0}=\) haben, kleiner als \(\varepsilon\) ist.