Kapitel 9: Grenzwerte (S. 127)

Aufgabe 1

(a)

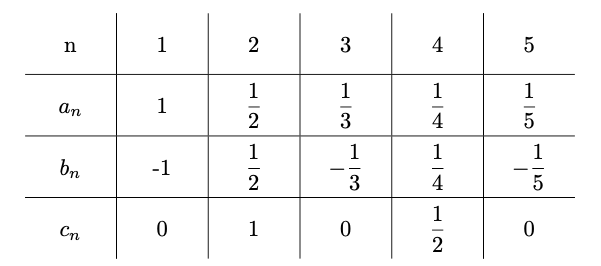
(b) Die Folgenglieder \(b_{n}\) werden kleiner als 0,001, wenn

\(\displaystyle (-1)^{n}\cdot\frac{1}{n}<0,001\,.\)

Ist n eine ungerade Zahl, so ist \(b_{n}\) negativ und damit sowieso kleiner als 0,001. Wir können uns also auf die geraden Zahlen konzentrieren, d.h. auf Zahlen der Form \(n=2m\). Dann ist

\(\displaystyle b_{n}=b_{2m}=(-1)^{2m}\cdot\frac{1}{2m}=\frac{1}{2m}\)

und

\(\displaystyle b_{2m}=\frac{1}{2m}<0,001\;\Longleftrightarrow\;2m>1000\;\Longleftrightarrow m>500\,.\)

Damit sind die Folgenglieder von \((b_{n})_{n}\) ab \(n=1001\) alle kleiner als 0,001. Kommen wir nun zur Folge \((c_{n})_{n}\). Für diese berechnen wir zunächst einmal eine etwas genauere Formel für die Folgenglieder:

\(\displaystyle c_{n}=a_{n}+b_{n}=\frac{1}{n}+(-1)^{n}\cdot\frac{1}{n}=\frac{1+(-1)^{n}}{n}=\left\{\begin{aligned}0\,\quad&,\quad n\text{ ungerade}\\\frac{2}{n}\quad&,\quad n\text{ gerade}\end{aligned}\right.\)

Entsprechend werden die Folgenglieder \(c_{n}\) kleiner als 0,001, wenn auch die geraden Folgenglieder kleiner als 0,001 werden, also

\(\frac{2}{n}<0,001\;\Longleftrightarrow\;n>\frac{1000}{2}=500\,\)

d.h. \(n=501\) ist.

(c) Wir starten mit \((b_{n})_{n}\). Gemäß der Definition von Seite 126, müssen wir zeigen, dass jeder zum vermeintlichen Grenzwert \(b=0\) vorgegebene Abstand \(\varepsilon\) irgendwann unterschritten wird. Sei also \(\varepsilon>0\) irgendein vorgegebener Abstand. Der tatsächliche Abstand zwischen den Folgengliedern \(b_{n}\) und dem vermeintlichen Grenzwert \(b=0\) ist ja gerade

\(\displaystyle|b_{n}-b|=\left|(-1)^{n}\cdot\frac{1}{n}-0\right|=\left|(-1)^{n}\cdot\frac{1}{n}\right|=\frac{1}{n}\,.\)

Die Frage ist also, ob es nun tatsächlich möglich ist, einen Index \(s\) zu finden, so dass

\(\displaystyle|b_{n}-b|=\frac{1}{n}<\varepsilon\) für alle \(n\geq s\)

ist. Das machen wir genauso wie in Aufgabenteil (b) und stellen diese Ungleichung einfach um. Zunächst einmal ist für \(n\geq s\):

\(n\geq s\;\Longleftrightarrow\;\frac{n}{s}\geq{1}\;\Longleftrightarrow\frac{1}{s}\geq\frac{1}{n}\,,\)

also reicht es, wenn wir die Nummer \(s\) so bestimmen, dass

\(\frac{1}{s}<\varepsilon\;\Longleftrightarrow\;s>\frac{1}{\varepsilon}\,.\)

ist. Und an genau dieser Stell verlassen wir jetzt den Bereich der Schulmathematik und wagen erste Schritte in die (Hochschul-)Mathematik. Das \(\varepsilon\) ist eine beliebig vorgegebene positive Zahl (soll ja ein Abstand sein), die wir eben nicht genau kennen; und wir müssen uns nun entscheiden, ob es nun zu dieser festen (aber eben unbekannten) Zahl eine Nummer (also eine natürliche Zahl) \(s\) gibt, die größer als \(\frac{1}{\varepsilon}\) ist. Versuchen wir uns einer Antwort zunächst mal intuitiv zu nähern:

Klar ist: für „große“ \(\varepsilon\) (also \(\varepsilon=10,100,1000,10000,\ldots\)) wird \(\frac{1}{\varepsilon}\) „klein“ (\(\frac{1}{\varepsilon}=0.1,0.01,0.001,0.0001,\ldots\)) und andersherum wird für „kleine“ \(\varepsilon\) (also \(\varepsilon=0.1,0.01,0.001,0.0001,\ldots\)) die Zahl \(\frac{1}{\varepsilon}\) „groß“ (\(\frac{1}{\varepsilon}=10,100,1000,10000,\ldots\)).

Die Zahl \(\frac{1}{\varepsilon}\) ist also immer positiv (weil \(\varepsilon\) positiv ist), kann aber beliebig groß sein. Unsere ursprüngliche Frage lautet also eigentlich: Gibt es zu jeder beliebigen Zahl \(z\) eine größere, natürliche Zahl \(s\)?

Intuitiv ist die Antwort: JA, aber klar!

(Wir nehmen einfach die Zahl z und runden sie bis zur nächst höheren natürlichen Zahl auf! – Aber geht das auch immer?)

Fragt man nun aber nach einem Beweis, also einer hieb- und stichfesten Begründung, muss man als ehrlicher Mathematiker zugestehen, dass wir hier schon fast vor einer philosophischen Frage stehen. Die Mathematik fußt auf einem System grundlegender Axiome (d.h. allgemein anerkannten Grundsätzen, die nicht aus der Theorie heraus abgeleitet werden können) und die Antwort auf obige Frage ist eines dieser Axiome. Das heißt: aus Sicht der Mathematik folgt man hier der intuitiven Vorstellung und legt einfach fest, dass eben diese Behauptung richtig ist. Das findet man dann in den Fachbüchern der Mathematik als das „Archimedische Axiom“.

Archimedisches Axiom: Die Menge der natürlichen Zahlen ist nach oben unbeschränkt, d.h. zu jeder reellen Zahl \(z\) existiert eine natürliche Zahl \(s\) mit \(s>z\).

Somit existiert auch für das gegebene (aber unbekannte) \(\varepsilon\), zu \(z=\frac{1}{\varepsilon}\in\mathbb{R}\) ein \(s\in\mathbb{N}\) mit \(s>z=\frac{1}{\varepsilon}\) und unsere Folge \((b_{n})_{n}\) hat somit tatsächlich den Grenzwert \(b=0\).

Ergänzung für den interessierten Leser:

Das archimedische Axiom ist nur ein Beispiel aus einem ganzen System von Axiomen, auf denen das Gerüst der modernen Mathematik heute steht. Alle Ergebnisse, Formeln und Theorien, die Mathematiker entwickeln und beherrschen sind letztlich aus diesen Axiomen abgeleitet. Darüber hinaus werden auch die Axiome selbst immer wieder hinterfragt und man kann auch andere Formen der Mathematik entwickeln, indem man einige dieser Axiome verwirft. Als kleines Beispiel kann man hier gut die ungeraden Wurzeln aus negativen Zahlen heranziehen. Tatsächlich ist es nämlich so (anders als man es vielleicht aus der Schule kennt), dass die Mathematik das Ziehen von Wurzeln (egal ob ungerade oder gerade) nur aus positiven Zahlen erlaubt, d.h.

so etwas wie \(\sqrt[3]{-27}\) gibt es aus Sicht der Mathematik nicht.

Der Grund dafür sind die Potenzgesetze. Würden wir solche Wurzeln zulassen, wäre

\(-2=\sqrt[3]{-8}=(-8)^{\frac{1}{3}}=(-8)^{\frac{2}{6}}=\sqrt[6]{(-8)^2}=\sqrt[6]{64}=2\,,\)

d.h. unsere Potenzgesetze gelten nicht mehr. Tatsächlich kann man sich nun also entscheiden;

entweder man folgt der „üblichen“ Mathematik, behält die Potenzgesetze und darf dafür keine Wurzeln (auch keine ungeraden) aus negativen Zahlen ziehen,
oder man versucht sich an einer „neuen“ Mathematik, behält die Wurzeln aus negativen Zahlen und verliert dafür die Potenzgesetze.

Die zweite Möglichkeit führt dann schnell auf sehr abstruse und abwägige Ergebnisse. Insbesondere werden Rechnungen dann sehr umständlich, so dass man (mit Blick auf den Zweck von Mathematik) doch bei der üblichen Mathematik bleibt. Grundsätzlich könnte man diesen Weg aber verfolgen.

Aufgabe 2

(a) Setzen wir zunächst Zahlen \(n=1,2,3,\ldots\) ein, erhalten wir

\(\displaystyle a_{1}=17-\frac{8}{1}=9,\quad a_{2}=17-\frac{8}{2}=13,\quad a_{3}=17-\frac{8}{3}=14\frac{1}{3},\quad\ldots\,,\)

die Werte nähern sich also anscheinend dem (Grenz-)Wert \(a=17\). Tatsächlich müssen wir zu vorgegebenem \(\varepsilon>0\) nur einen Index \(s\) größer als \(\frac{8}{\varepsilon}\) wählen (nach der ausführlichen Erklärung in Aufgabe 1 ist das immer möglich) und für jedes \(n>s\) folgt:

\(a_n-a=17-\frac{8}{n}-17=-\frac{8}{n}>-\frac{8}{s}>-\frac{8}{8/\varepsilon}=-\varepsilon\)

(beachte, dass mit Verkleinerung des Nenners ein Bruch größer wird – man teilt ja durch eine geringere Zahl). Außerdem gilt sowieso

\(a_n-a=17-\frac{8}{n}-17=-\frac{8}{n}<0<\varepsilon\,.\)

Der Grenzwert ist also wirklich \(a=17\).

(b) Für die ersten paar Glieder der Folge erhalten wir

\(\displaystyle b_{1}=1+\frac{1}{1}=2,\quad b_{2}=2+\frac{1}{2}=\frac{5}{2},\quad b_{3}=3+\frac{1}{3}=\frac{10}{3},\quad\ldots\,,\)

die Werte werden also immer größer. Genauer gesagt ist

\(a_{n}=n+\frac{1}{n}>n\)

und da gemäß des Archimedischen Axioms zu jeder beliebigen Zahl \(z>0\) eine natürliche Zahl \(n\) existiert mit \(n>z\), wird \(a_{n}\) beliebig groß, nähert sich also keinem Wert an. Entsprechend hat die Folge keinen Grenzwert.

\(\displaystyle c_{1}=\frac{1+8}{3\cdot1-1}=4,\quad c_{2}=\frac{2+8}{3\cdot2-1}=2,\quad c_{3}=\frac{3+8}{3\cdot3-1}=1,375,\quad\ldots,\)

die Werte werden also beständig kleiner. Da wir aber nur natürliche Zahlen einsetzen, bleiben sowohl Zähler als auch Nenner immer nichtnegativ. Es lässt sich also vermuten, dass auch hier ein Grenzwert existiert. Tatsächlich können wir in diesem Fall den Term ein bisschen Umformen und so den Grenzwert praktisch ablesen:

\(\displaystyle \frac{n+8}{3\cdot n-1}=\frac{n\cdot\left(1+8\cdot\frac{1}{n}\right)}{n\cdot\left(3-\frac{1}{n}\right)}=\frac{1+8\cdot\frac{1}{n}}{3-\frac{1}{n}}\)

Wir wissen ja bereits aus Aufgabe 1, dass die Folge \((\frac{1}{n})\) den Grenzwert Null hat. Entsprechend sollte unsere Folge \((c_{n})\) den Grenzwert

\(\displaystyle c=\frac{1+8\cdot 0}{3-0}=\frac{1}{3}\)

haben. Tatsächlich gilt:

\(\displaystyle c_{n}-c=\frac{n+8}{3\cdot n-1}-\frac{1}{3}=\frac{3\cdot(n+8)}{3\cdot(3\cdot n-1)}-\frac{3n-1}{3\cdot(3n-1)}=\frac{25}{9n-3}<\frac{25}{9n-3n}<\frac{25}{6n}\)

Wählen wir also zu \(\varepsilon>0\) den Index \(s\) so, dass \(s>\frac{25}{6\varepsilon}\) (Archimedisches Axiom), folgt für \(n>s\):

\(\displaystyle-\varepsilon<0<\frac{25}{9n-3}=c_{n}-c<\frac{25}{6n}<\frac{25}{6s}<\frac{25}{6\cdot(\frac{25}{6\varepsilon})}=\varepsilon\,.\)