Kapitel 8: Funktionen (S. 107)
Aufgabe 1
(a) Den Scheitelpunkt kannst du aus der Funktionsgleichung ablesen. Es gilt \(d=-2\) und \(e=-3\). Somit hat der Scheitelpunkt die Koordinaten \((-2|-3)\). Da \(a=1\) gilt, ist die Parabel nach oben geöffnet. Genauer handelt es sich sogar um die um 2 Einheiten in x-Richtung und 3 Einheiten in y-Richtung verschobene Normalparabel.
Aus diesen Informationen kannst du den folgenden Graphen ableiten:
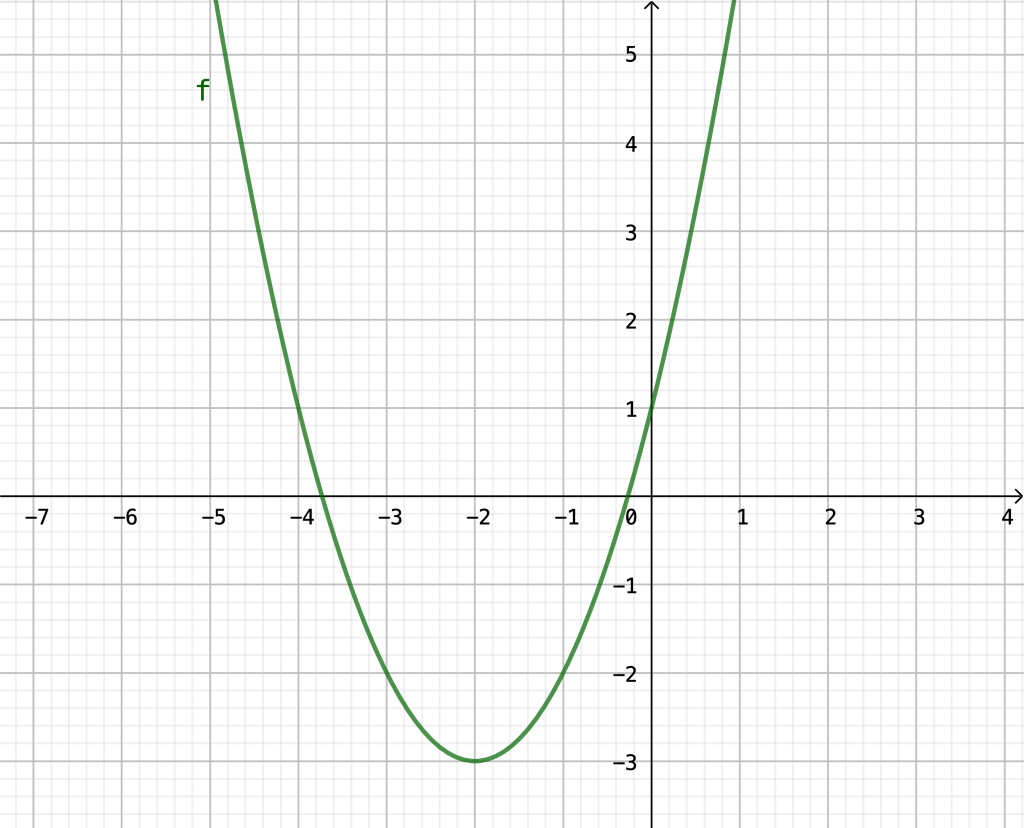
Die Normalform erhältst du, indem du die gegebene Scheitelpunktform vollständig ausmultiplizierst:
\(f(x)=(x+2)^2-3=x^2+4x+4-3=x^2+4x+1\)(b) Hier können wir im Wesentlichen genau so vorgehen. Es gilt \(d=4\) und \(e=3\). Der Scheitelpunkt hat also die Koordinaten \((4|3)\). Da jetzt \(a=-2\) gilt, ist die Parabel nach unten geöffnet. Den Graphen kannst du gut skizzieren, wenn du noch 2 bis 4 weitere Punkte anhand des Funktionsterms berechnest. Hierzu setzt du einfach beliebige Werte für \(x\) ein und schaust, was du für \(g(x)\) erhältst. Der Graph sieht dann so aus:
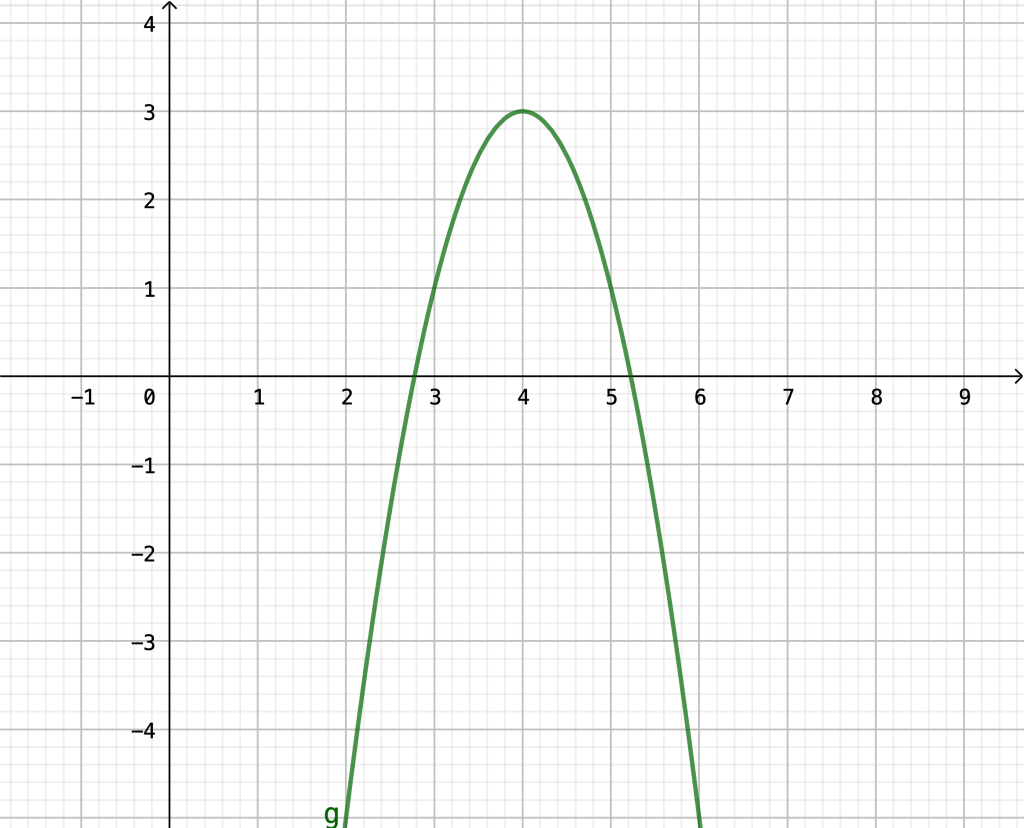
Die Normalform lautet \(g(x)=-2(x-4)^2+3=-2(x^2-8x+16)+3=-2x^2+16x-32+3=-2x^2+16x-29\).
Aufgabe 2
(a) Damit wir die quadratische Ergänzung wie in Kapitel 5 (S. 64) durchführen können, darf kein Vorfaktor mehr vor \(x^2\). Da dies hier nicht der Fall ist, können wir direkt loslegen:
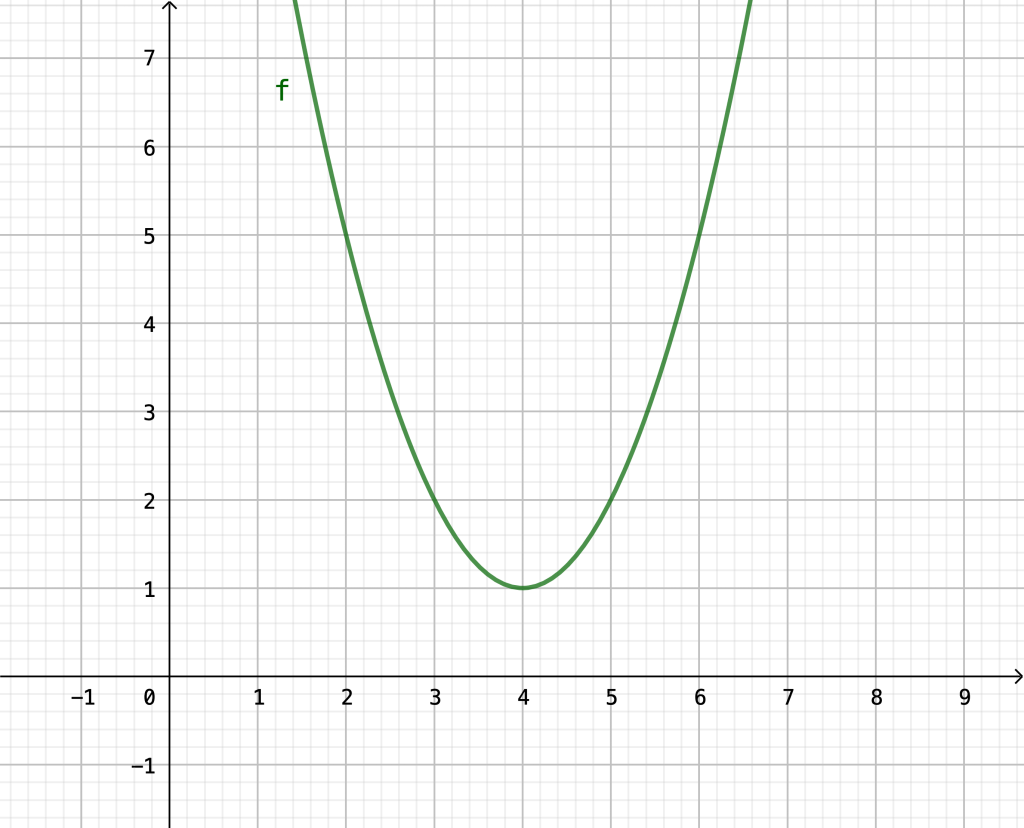
\(f(x)=x^2-8x+17=x^2-8x+16+1=(x-4)^2+1\)Nun kannst du wieder \(d=4\) und \(e=1\) ablesen, so dass der Scheitelpunkt \((4|1)\) beträgt.
Als Graph erhältst du folgenden:
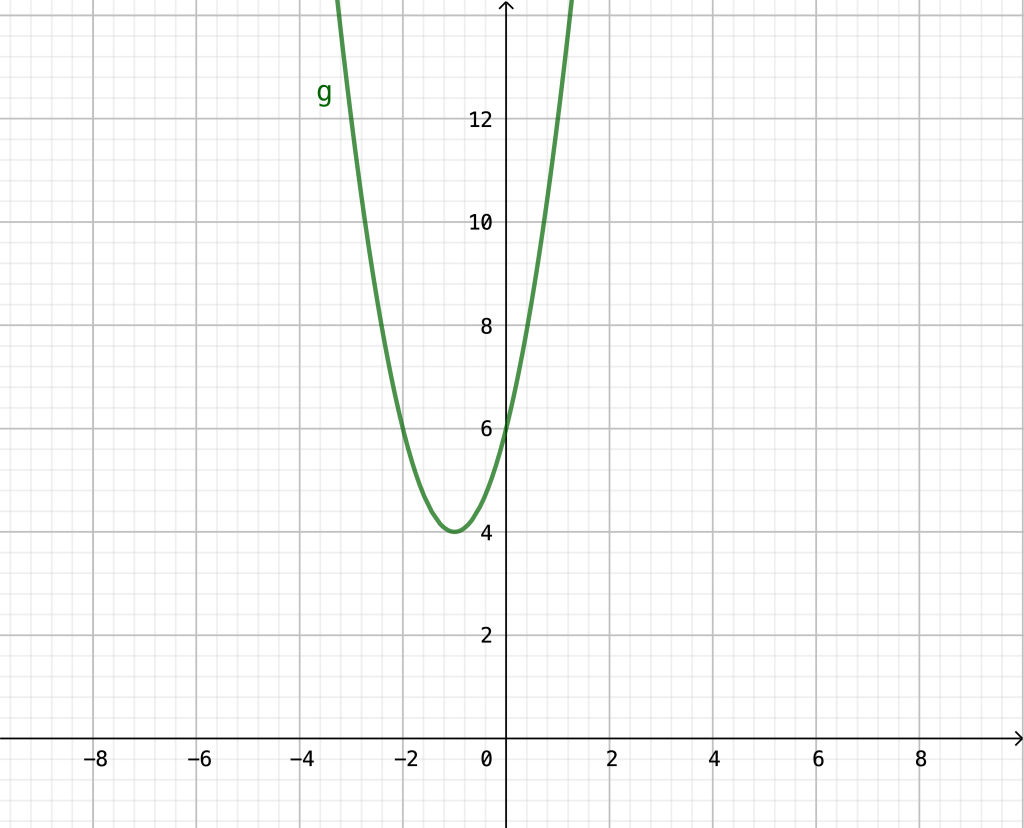
(b) Die Funktion \(g\) hat den Vorfaktor \(2\) vor \(x^2\). Wir klammern diesen zunächst aus und konzentrieren uns nur auf den Teil, der übrig bleibt. Anschließend multiplizieren wir den Faktor wieder zurück.
\(g(x)=2x^2+4x+6=2(x^2+2x+3)=2((x+1)^2+2)=2(x+1)^2+4\)Hieraus erhalten wir \(d=-1\) und \(e=4\), so dass der Scheitelpunkt \((-1|4)\) beträgt.
Der Graph sieht dann so aus: