Kapitel 8: Funktionen (S. 121)
Aufgabe 1
(a) Die Funktion ist überall stetig.
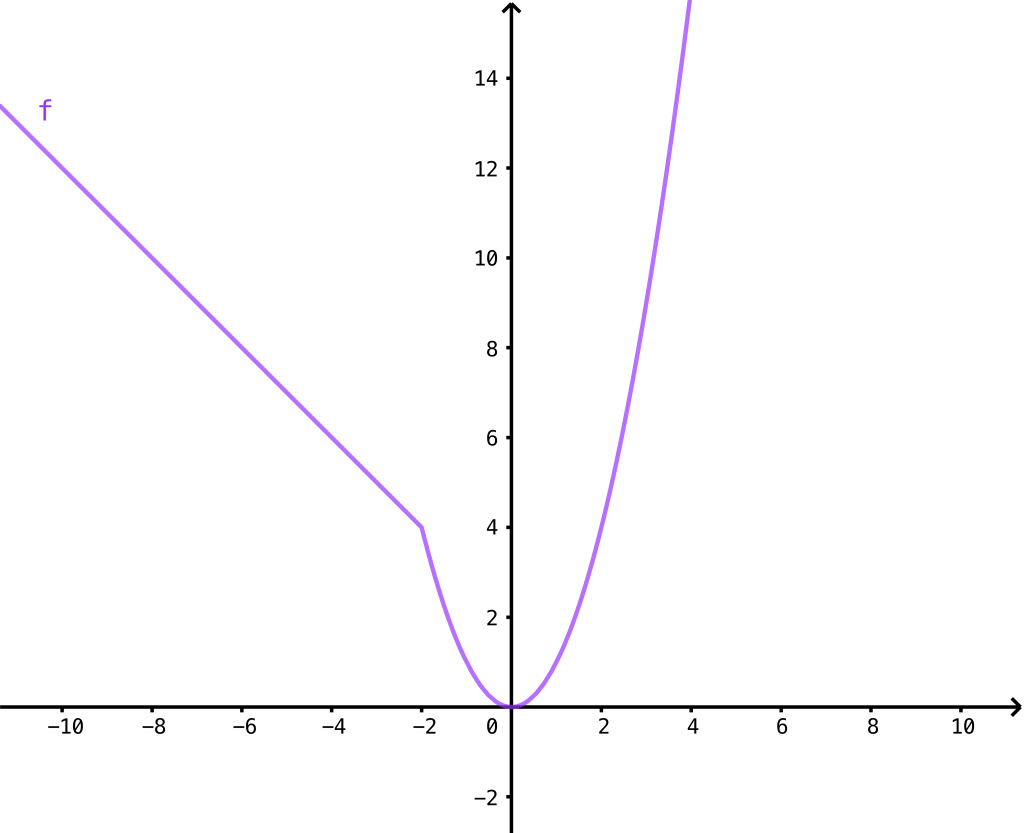
(b) Die Funktion ist jeweils an den Nahtstellen zwischen den unterschiedlichen Funktionstermen (d. h. bei -2 und 1) unstetig.
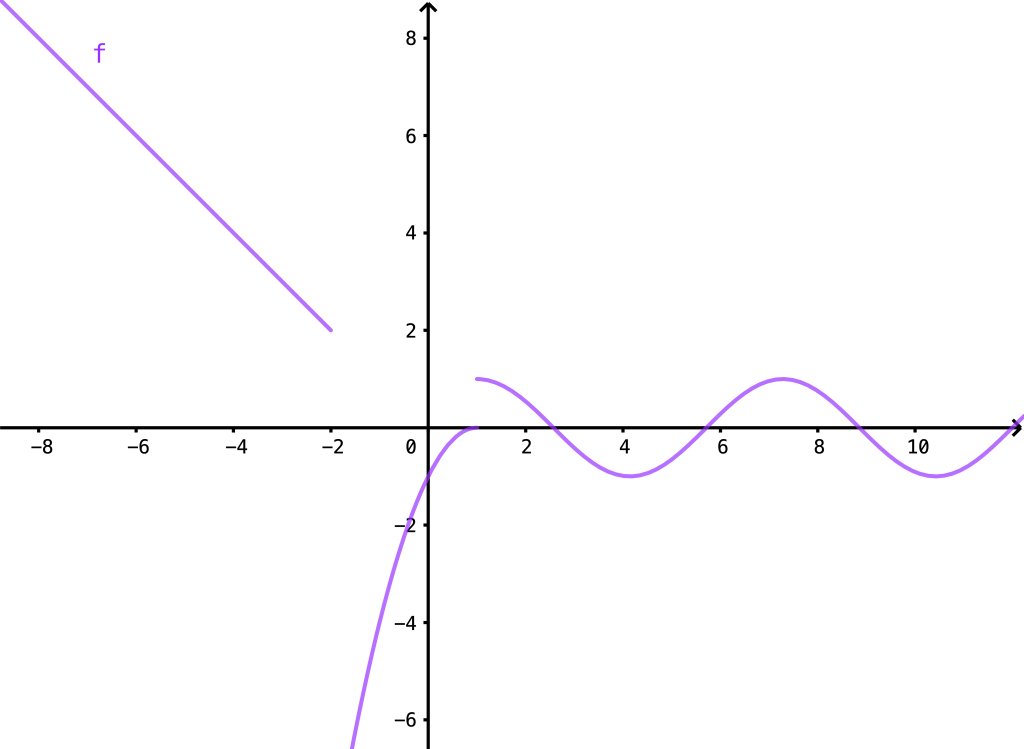
Aufgabe 2
(a) \(f(x)=\left\{\begin{array}{lr}x+3 & x<-2\\\frac{x^2}{4} & -2\le x \le 2\\1 & x>2\\\end{array}\right.\)
(b) \(g(x)=\left\{\begin{array}{lr}-x^2+1 & x<0\\2^x & 0\le x \le 2\\x-2 & x>2\\\end{array}\right.\)