Kapitel 8: Funktionen (S. 103)
Aufgabe 1
- \(f(x)=2x+1\) ist eine lineare Funktion.
- \(g(t)=2t^2+3\) ist eine quadratische Funktion. Ihr Funktionsgraph ist eine Parabel.
- \(f(x)=x^2\) ist eine quadratische Funktion. Auch ihr Funktionsgraph ist eine Parabel, und zwar eine spezielle: die sog. Normalparabel.
- \((a)=x\) ist eine lineare Funktion. Lineare Funktionen ohne einen hinzuaddierten Wert nennt man auch proportionale Funktionen.
- \(h(x)=3^x\) ist eine Exponentialfunktion.
- \(g(x)=\log(2x)\) ist eine Logarithmusfunktion.
- \(p(x)=x^3+2x^2-x+3\) ist eine Polynomfunktion.
Sowohl lineare als auch quadratische Funktionen kann man zudem als Polynomfunktionen auffassen. \(f(x)=x^2\) kann man zudem auch als Potenzfunktion auffassen.
Aufgabe 2
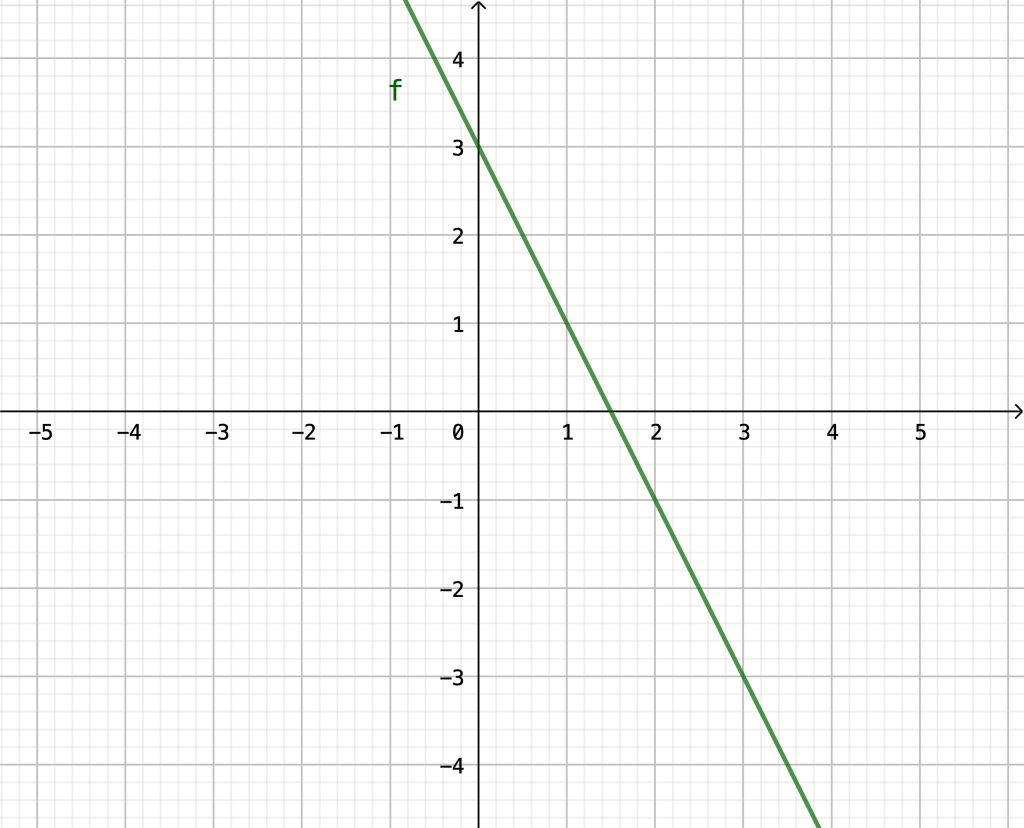
(a) Eine Tabelle kann z. B. so aussehen:

Das ist natürlich immer auch davon abhängig, welche \(x\)-Werte du wählst.
Der Funktionsgraph sieht so aus:
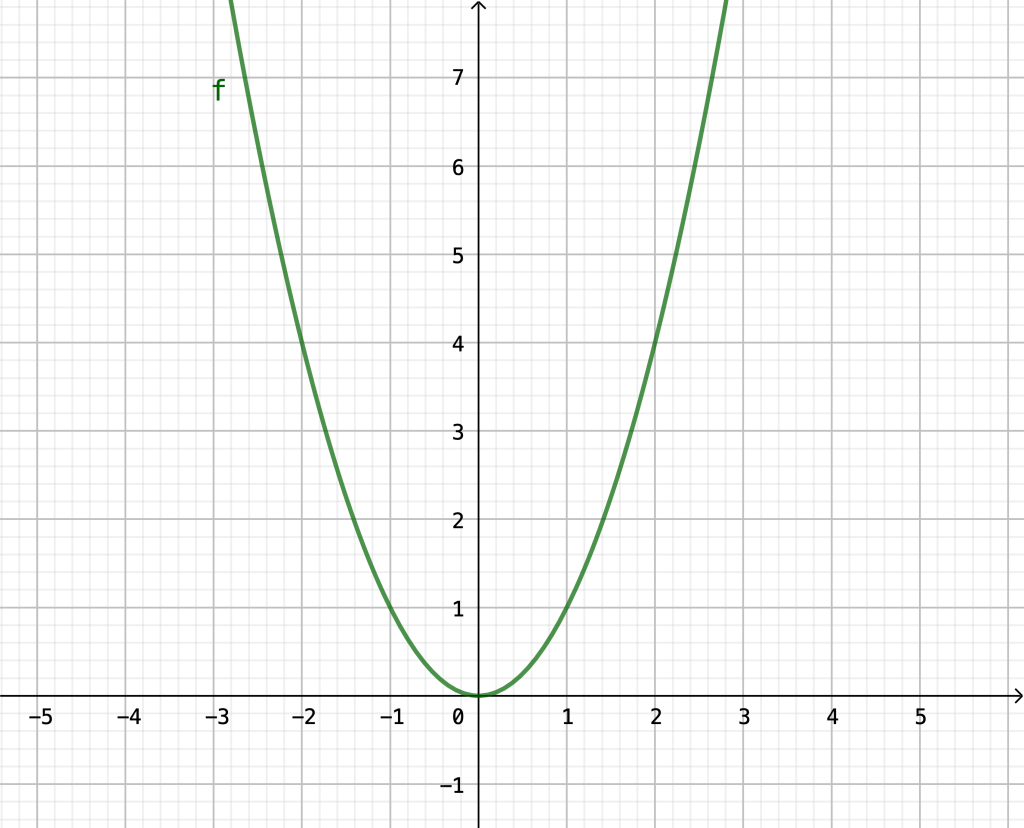
(b) Z. B. durch ein wenig Knobeln und die Zusatzinfo, dass es sich um eine quadratische Funktion handeln soll, kann man erraten, dass der Funktionsterm \(f(x)=x^2\) passt. Der Graph ist die sog. Normalparabel:
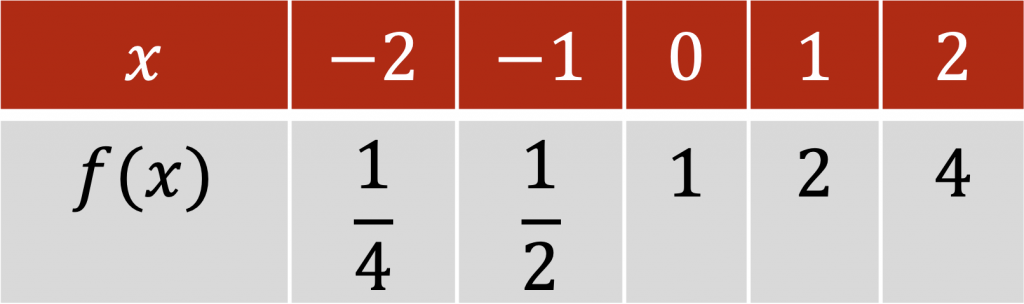
(c) Anhand des gegebenen Funktionsgraphs kann man die Wertepaare \(f(0)=1\), \(f(1)=2\) sowie \(f(2)=4\) ablesen. Außerdem wächst die Funktion sehr schnell, wenn man den Graph von links nach rechts verfolgt.
Auch hier kommt man wieder durch Knobeln auf \(f(x)=2^x\).
Eine Wertetabelle kann dann z. B. so aussehen: