Kapitel 7: Satz des Pythagoras und Trigonometrie (S. 98)
Aufgabe 1
(a) Aus der Innenwinkelsumme folgt zunächst (nach Umrechnung von \(\gamma\) ins Gradmaß):
\(\alpha=180^{\circ}-\beta-\gamma=180^{\circ}-43^{\circ}-20^{\circ}=117^{\circ}\,.\)
Mit dem Sinussatz berechnen wir dann die Längen der Seiten \(a\) und \(b\). Es ist
\(\displaystyle\frac{a}{\sin(\alpha)}=\frac{c}{\sin(\gamma)}\;\Longleftrightarrow\;a=\frac{c}{\sin(\gamma)}\cdot\sin(\alpha)=\frac{17,9\,\text{cm}}{\sin\left(20^{\circ}\right)}\cdot\sin(117^{\circ})\approx46,63\,\text{cm}\,.\)
und
\(\displaystyle\frac{b}{\sin(\beta)}=\frac{c}{\sin(\gamma)}\;\Longleftrightarrow\;b=\frac{c}{\sin(\gamma)}\cdot\sin(\beta)=\frac{17,9\,\text{cm}}{\sin\left(20^{\circ}\right)}\cdot\sin(43^{\circ})\approx35,69\,\text{cm}\,.\)
Damit können wir eine grobe Skizze des Dreiecks anfertigen:
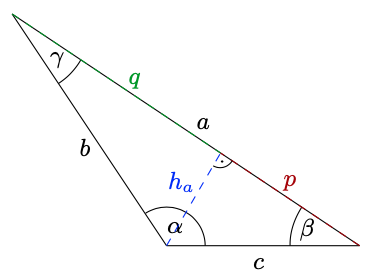
Für den Flächeninhalt benötigen wir nun schließlich noch eine Höhe, zum Beispiel die Höhe \(h_{a}\). Dafür entnehmen wir der obigen Skizze, dass
\(\displaystyle a=p+q\;\qquad\tan(\beta)=\frac{h_{a}}{p}\,,\qquad\tan(\gamma)=\frac{h_{a}}{q}\,,\)
also
\(\begin{align*}&\hspace{-0.5cm}\displaystyle a=\frac{h_{a}}{\tan(\beta)}+\frac{h_{a}}{\tan(\gamma)}\\&\Longleftrightarrow\;h_{a}=a\cdot\frac{\tan(\beta)\cdot\tan(\gamma)}{\tan(\beta)+\tan(\gamma)}\approx46,63\,\text{cm}\cdot\frac{\tan(20^{\circ})\cdot\tan(43^{\circ})}{\tan(20^{\circ})+\tan(43^{\circ})}\approx12,21\,\text{cm}\,.\end{align*}\)
Damit erhalten wir für den Flächeninhalt des Dreiecks:
\(\displaystyle A=\frac{1}{2}\cdot a\cdot h_{a}\approx\frac{1}{2}\cdot46,63\,\text{cm}\cdot12,21\,\text{cm}\approx284,68\,\text{\cm}^2\)
(b) Mit dem Sinussatz erhalten wir zunächst den Winkel \(\beta\):
\(\begin{align*}\frac{a}{\sin(\alpha)}=\frac{b}{\sin(\beta)}&\;\Longleftrightarrow\;\sin(\beta)=\frac{\sin(\alpha)}{a}\cdot b\\&\;\Longleftrightarrow\;\beta=\arcsin\left(\frac{\sin(\alpha)}{a}\cdot b\right)=\arcsin\left(\frac{\sin(55^{\circ})}{12,9\,\text{cm}}\cdot1\,\text{cm}\right)\approx3,64^{\circ}\,.\end{align*}\)
Die Innenwinkelsumme liefert dann
\(\gamma=180^{\circ}-\alpha-\beta\approx180^{\circ}-55^{\circ}-3,64^{\circ}=121,36^{\circ}\,,\)
und mit erneuter Anwendung des Sinussatzes zum Einen
\(\displaystyle\frac{a}{\sin(\alpha^{\circ})}=\frac{b}{\sin(\beta)}\;\Longleftrightarrow\;b=\frac{a}{\sin(\alpha)}\cdot\sin(\beta)\approx\frac{12,9\,\text{cm}}{\sin(55^{\circ})}\cdot\sin(3,64^{\circ})\approx1\,\text{cm}\,,\)
sowie zum Anderen:
\(\displaystyle\frac{a}{\sin(\alpha^{\circ})}=\frac{c}{\sin(\gamma)}\;\Longleftrightarrow\;c=\frac{a}{\sin(\alpha)}\cdot\sin(\gamma)\approx\frac{12,9\,\text{cm}}{\sin(55^{\circ})}\cdot\sin(121,36^{\circ})\approx13,45\,\text{cm}\,.\)
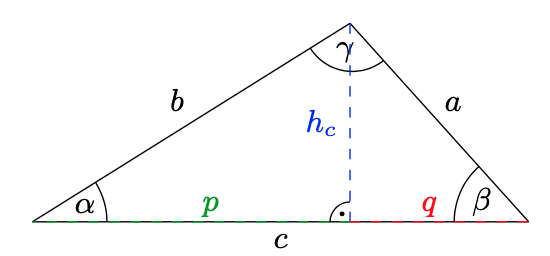
Wie in (a) benötigen wir für den Flächeninhalt erneut eine Höhe. Wählen wir diesmal die Höhe \(h_{c}\), folgt aus der Skizze:
\(\displaystyle c=p+q\;\qquad\tan(\alpha)=\frac{h_{c}}{p}\,,\qquad\tan(\beta)=\frac{h_{c}}{q}\,,\)
also
\(\begin{align*}&\hspace{-0.5cm}c=\frac{h_{c}}{\tan(\alpha)}+\frac{h_{c}}{\tan(\beta)}\\&\Longleftrightarrow\;h_{c}=c\cdot\frac{\tan(\alpha)\cdot\tan(\beta)}{\tan(\alpha)+\tan(\beta)}\approx13,45\,\text{cm}\cdot\frac{\tan(55^{\circ})\cdot\tan(3,64^{\circ})}{\tan(55^{\circ})+\tan(3,64^{\circ})}\approx1,82\,\text{cm}\,.\end{align*}\)
und damit folgt für den Flächeninhalt:
\(A=\frac{1}{2}\cdot c\cdot h_{c}\approx\frac{1}{2}\cdot 13,45\,\text{cm}\cdot1,82\,\text{cm}\approx12,24\,\text{cm}^2\,.\)
(c) Dieses Dreieck ist offensichtlich rechtwinklig, da \(\gamma=\frac{\pi}{2}=90^{\circ}\). Damit gilt in diesem Dreieck der Satz des Pythagoras und wir erhalten für die Hypothenuse:
\(c^2=a^2+b^2\;\Longleftrightarrow\;c=\sqrt{a^2+b^2}=\sqrt{\left(3\,\text{dm}\right)^2+\left(8,9\,\text{dm}\right)^2}=\sqrt{88,21}\,\text{dm}\approx9,39\,\text{dm}\,.\)
Damit folgt für den Winkel \(\alpha\) (zum Beispiel mit dem Kosinus)
\(\displaystyle\cos(\alpha)=\frac{b}{c}\;\Longleftrightarrow\;\alpha=\arccos\left(\frac{b}{c}\right)=\arccos\left(\frac{8,9\,\text{dm}}{\sqrt{88,21}\,\text{dm}}\right)\approx18,63^{\circ}\,,\)
und mit der Innenwinkelsumme erhalten wir schließlich
\(\beta=180^{\circ}-\gamma-\alpha\approx180^{\circ}-90^{\circ}-18,63^{\circ}=71,37^{\circ}\,.\)
Da das Dreieck rechtwinklig ist, ist zudem die Seite \(a\) gleichzeitig die Höhe \(h_{b}\) bezogen auf die Grundseite \(b\). Damit ist der Flächeninhalt:
\(\displaystyle A=\frac{1}{2}\cdot b\cdot a=\frac{1}{2}\cdot 8,9\,\text{dm}\cdot 3\,\text{dm}=13,35\,\text{dm}^2\,.\)
Aufgabe 2
Für die Gesamtlänge des Zauns benötigen wir noch die Längen der Seiten \(c\) und \(d\). Aus dem Kosinussatz folgt:
\(\begin{alignat*}{3}&&c^2+b^2-2\cdot b\cdot c\cdot\cos(\beta)&=f^2\qquad&&|\;-b^2\\&\Longleftrightarrow\quad&c^2-2\cdot c\cdot b\cdot\cos(\beta)&=f^2-b^2\qquad&&|\;\text{quadr. Ergänzung}\\&\Longleftrightarrow\quad &c^2-2\cdot c\cdot b\cdot\cos(\beta)+\left(b\cdot\cos(\beta)\right)^2&=f^2-b^2+\left(b\cdot\cos(\beta)\right)^2\qquad&&\\&\Longleftrightarrow\quad&\left(c-b\cdot\cos(\beta)\right)^2&=f^2-b^2(1-\cos^2(\beta))&&\\&\Longleftrightarrow\quad&\left(c-b\cdot\cos(\beta)\right)^2&=f^2-b^2\cdot\sin^2(\beta)\qquad&&|\;\sqrt{\;\;\,}\\&\Longleftrightarrow\quad&c-b\cdot\cos(\beta)&=\pm\sqrt{f^2-b^2\sin^2(\beta)}\qquad&&\Big|\;+b\cdot\cos(\beta)\\&\Longleftrightarrow\quad&c=b\cdot\cos(\beta)\pm\sqrt{f^2-b^2\sin^2(\beta)}\,.&&\end{alignat*}\)
Da Längen positiv sind entfällt die negative Lösung und wir erhalten:
\(c=85,8\,\text{m}\cdot\cos(87^{\circ})+\sqrt{\left(214\,\text{m}\right)^2-(85,8\,\text{m})^2\sin^2(87^{\circ})^2}\approx220,59\,\text{m}\,.\)
Ersetzen wir nun in obiger Formel den Winkel \(\beta\) durch \(\alpha\) und \(b,c\) durch \(a,d\), erhalten wir
\(\displaystyle d=a\cdot\cos(\alpha)\pm\sqrt{f^2-a^2\sin^2(\alpha)}\)
und da wir wieder nur die positive Lösung berücksichtigen müssen, folgt
\(c=128,5\,\text{m}\cdot\cos(60^{\circ})+\sqrt{\left(214\,\text{m}\right)^2-(128,5\,\text{m})^2\sin^2(60^{\circ})^2}\approx247,04\,\text{m}\,.\)
Insgesamt hat der Zaun also eine Länge von
\(L=a+b+c+d\approx128,5\,\text{m}+85,8\,\text{m}+220,59\,\text{m}+247,04\,\text{m}=681,93\,\text{m}\,.\)
Aufgabe 3
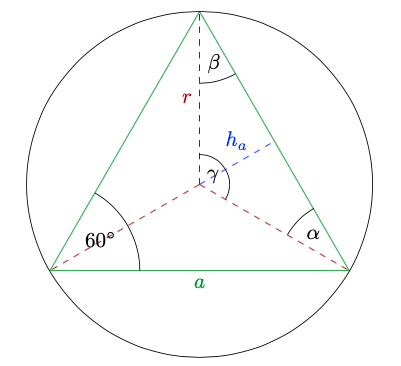
(a) Das gleichseitige Dreieck lässt sich durch den Radius in drei deckungsgleiche Dreiecke zerlegen (siehe Skizze). Aufgrund der Symmetrie sind die Winkel \(\alpha\) und \(\beta\) in diesen Dreiecken gleich groß und es gilt gerade:
\(\alpha=\beta=30^{\circ}\,.\)
Mit der Innenwinkelsumme folgt für den Winkel \(\gamma\) gerade
\(\gamma=180^{\circ}-\alpha-\beta=180^{\circ}-30^{\circ}-30^{\circ}=120^{\circ}\,,\)
und der Sinussatz liefert
\(\displaystyle\frac{r}{\sin(\alpha)}=\frac{a}{\sin(\gamma)}\;\Longleftrightarrow\;r=\frac{a}{\sin(\gamma)}\cdot\sin(\alpha)=\frac{24\,\text{cm}}{\sin(120^{\circ})}\cdot\sin(30^{\circ})\approx13,86\,\text{cm}\,.\)
(b) Der Flächeninhalt des Pfeils ist gerade das Doppelte des Flächeninhalts der deckungsgleichen Dreiecke. Diese sind gleichschenklig (die beiden Schenkel entsprechen ja dem Radius) und damit erhalten wir für die Höhe gerade
\(\displaystyle\tan(\alpha)=\frac{h_{a}}{\frac{a}{2}}\;\Longleftrightarrow\;h_{a}=\frac{a}{2}\cdot\tan(\alpha)=12\,\text{cm}\cdot\tan(30^{\circ})\approx 6,93\,\text{cm}\,.\)
Damit hat der Pfeil einen Flächeninhalt von
\(\displaystyle A=2\cdot\frac{1}{2}\cdot a\cdot h_{a}=a\cdot h_{a}\approx24\,\text{cm}\cdot6,93\,\text{cm}\approx166,32\,\text{cm}^2\,.\)
Aufgabe 4
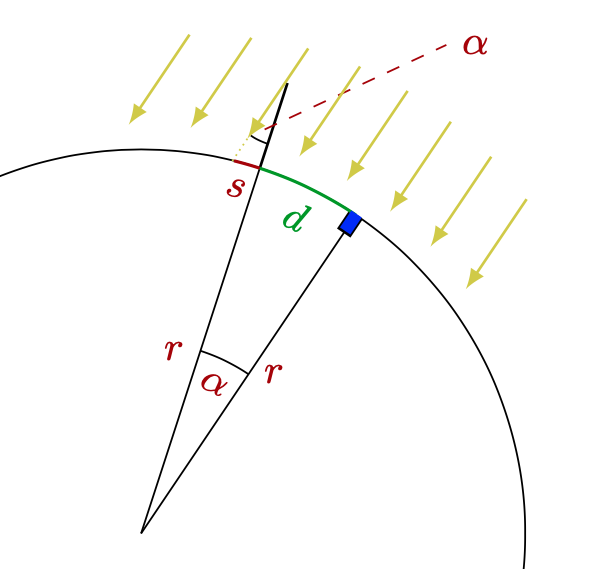
Hier fehlt als Angabe die Länge des Schattens, die Eratosthenes gemessen hat. Das waren etwa \(19\,\text{m}\). Damit lässt sich nun der Winkel \(\alpha\) bestimmen unter der die Sonnenstrahlen in Alexandria den Obelisken passieren:
\(\displaystyle\tan(\alpha)=\frac{s}{h}\,.\)
Berücksichtigen wir, dass aufgrund der Entfernung von der Erde zur Sonne, die Sonnenstrahlen auf der Erde nahezu parallel eintreffen, entspricht \(\alpha\) dem Winkel zwischen den Erdradien, die jeweils Alexandria bzw. Syene mit dem Erdmittelpunkt verbinden (siehe Skizze).
Zudem „misst“ die Entfernung von Alexandria nach Syene den Winkel \(\alpha\) im Bogenmaß. Genauer gesagt gilt (vgl. Definition des Bogenmaß auf Seite 88):
\(\displaystyle \frac{\alpha}{2\pi}=\frac{d}{2\pi r}\;\Longleftrightarrow\; r=\frac{d}{\alpha}\,.\)
und somit
\(\displaystyle r=\frac{d}{\alpha}=\frac{d}{\arctan\left(\frac{s}{h}\right)}=\frac{800\,\text{km}}{\arctan\left(\frac{19\,\text{m}}{150\,\text{m}}\right)}\approx6349,42\,\text{km}\,.\)
Vergleicht man diesen Wert mit den durch moderne Methoden bestimmten Erdradius von \(r_{mod}\approx 6371\,\text{km}\), liegt Eratosthenes tatsächlich um nur \(21,58\,\text{km}\) daneben.
Aufgabe 4
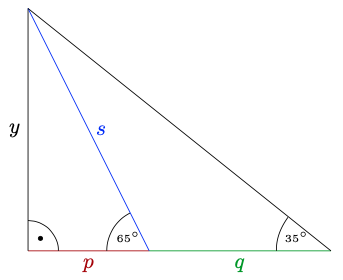
Aus der Skizze können wir ablesen, dass
\(\displaystyle\frac{y}{p}=\tan(\beta)\quad\) und \(\quad\displaystyle\frac{y}{p+q}=\tan(\alpha)\,,\)
also
\(\displaystyle\tan(\beta)\cdot p=\tan(35^{\circ})\cdot(p+q)\;\Longleftrightarrow\;p=q\cdot\frac{\tan(\alpha)}{\tan(\beta)-\tan(\alpha)}\,.\)
Außerdem gilt für den gesuchten Abstand \(s\):
\(\displaystyle\cos(\beta)=\frac{p}{s}\;\Longleftrightarrow\;s=\frac{p}{\cos(\beta)}\)
und setzen wir \(p\) ein, folgt mit \(q=6,2\,\text{sm}\) schließlich:
\(\displaystyle s=q\cdot\frac{\tan(\alpha)}{\cos(\beta)\cdot\left(\tan(\beta)-\tan(\alpha)\right)}=6,2\,\text{sm}\cdot\frac{\tan(35^{\circ})}{\cos(61^{\circ})\cdot\left(\tan(61^{\circ})-\tan(35^{\circ})\right)}\approx8,11\,\text{sm}\,.\)