Kapitel 7: Satz des Pythagoras und Trigonometrie (S. 95)
Aufgabe 1

Die fehlenden Größen lassen sich direkt mit dem Sinussatz von S. 94 berechnen:
(a) Zunächst einmal ist
\( \displaystyle\frac{a}{\sin(\alpha)}=\frac{b}{\sin(\beta)}\;\Longleftrightarrow\;\beta=\arcsin\left(\frac{b}{a}\cdot\sin(\alpha)\right)=\arcsin\left(\frac{4,5\,\text{cm}}{6\,\text{cm}}\cdot\sin(75^{\circ})\right)\approx46,42^{\circ}\,.\)
Nun liefert die Innenwinkelsumme \(\gamma=180^{\circ}-\alpha-\beta\approx180^{\circ}-75^{\circ}-46,42^{\circ}=58,58^{\circ}\) und erneut folgt aus dem Sinussatz
\( \displaystyle\frac{a}{\sin(\alpha)}=\frac{c}{\sin(\gamma)}\;\Longleftrightarrow\;c=\frac{a}{\sin(\alpha)}\cdot\sin(\gamma)\approx\frac{6\,\text{cm}}{\sin(75^{\circ})}\cdot\sin(58,58^{\circ})\approx5,3\,\text{cm}\,.\)
(b) Wieder liefert der Sinussatz zunächst
\(\displaystyle \frac{c}{\sin(\gamma)}=\frac{b}{\sin(\beta)}\;\Longleftrightarrow\;\gamma=\arcsin\left(\frac{c}{b}\cdot\sin(\beta)\right)=\arcsin\left(\frac{5,5\,\text{cm}}{6,2\,\text{cm}}\cdot\sin(0,6\,\pi)\right)\approx0,32\,\pi\,.\)
Nun liefert die Innenwinkelsumme \(\alpha=\pi-\beta-\gamma \approx\pi-0,6\,\pi-0,32\,\pi=0,08\,\pi\) und erneut folgt aus dem Sinussatz
\(\displaystyle \frac{a}{\sin(\alpha)}=\frac{b}{\sin(\beta)}\;\Longleftrightarrow\;a=\frac{b}{\sin(\beta)}\cdot\sin(\alpha)\approx\frac{6,2\,\text{cm}}{\sin(0,6\,\pi)}\cdot\sin(0,08\,\pi)\approx1,62\,\text{cm}\,.\)
(c) Es ist
\(\displaystyle \frac{a}{\sin(\alpha)}=\frac{c}{\sin(\gamma)}\;\Longleftrightarrow\;\alpha=\arcsin\left(\frac{a}{c}\cdot\sin(\gamma)\right)=\arcsin\left(\frac{5\,\text{cm}}{3,2\,\text{cm}}\cdot\sin\left(\frac{\pi}{6}\right)\right)\approx0,29\,\pi\,.\)
Nun liefert die Innenwinkelsumme \(\beta=\pi-\alpha-\gamma\approx\pi-0,29\,\pi-\frac{\pi}{6}\approx0,54\,\pi\) und erneut folgt aus dem Sinussatz
\( \displaystyle\frac{b}{\sin(\beta)}=\frac{c}{\sin(\gamma)}\;\Longleftrightarrow\;b=\frac{c}{\sin(\gamma)}\cdot\sin(\beta)\approx\frac{3,2\,\text{cm}}{\sin\left(\frac{\pi}{6}\right)}\cdot\sin(0,29\,\pi)\approx6,35\,\text{cm}\,.\)
Aufgabe 2
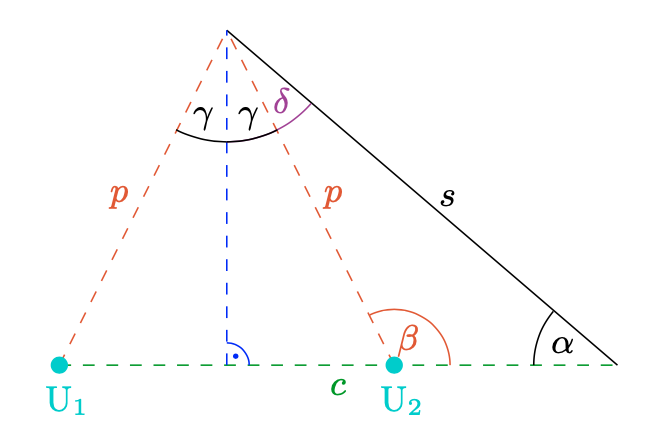
Für den Winkel \(\alpha\) in der Skizze liefert die Aufgabenstellung gerade
\(\alpha=90^{\circ}-\epsilon=90^{\circ}-35^{\circ}=55^{\circ}\,.\)
Mit dem Sinussatz lässt sich nun zunächst einmal eine Formel zur Berechnung von \(\beta\) ableiten (beachte, dass \(\beta>90^{\circ}\)):
\(\begin{align*}&\hspace{-0.5cm}\frac{s}{\sin(\beta)}=\frac{p}{\sin(\alpha)}\\&\;\Longleftrightarrow\;\beta=\arcsin\left(\frac{s}{p}\cdot\sin(\alpha)\right)\\&\phantom{\;\Longleftrightarrow\;\beta\;}=\arcsin\left(\frac{90\,\text{cm}}{80\,\text{cm}}\cdot\sin(55^{\circ})\right)\approx112,85^{\circ}\,.\end{align*}\)
Damit ist dann der Winkel \(\delta\) gemäß Innenwinkelsumme gerade
\(\delta=180^{\circ}-\alpha-\beta\approx180^{\circ}-55^{\circ}-112,85^{\circ}=12,15^{\circ}\,,\)
und außerdem liefert die Innenwinkelsumme:
\(\gamma+\delta=90^{\circ}-\alpha\;\Longleftrightarrow\;\gamma=90^{\circ}-\alpha-\delta\approx90^{\circ}-55^{\circ}-12,15^{\circ}=22,85^{\circ}\,.\)
Wenden wir nun den Sinussatz auf das „große Dreieck“ an, folgt:
\(\displaystyle\frac{c}{\sin(2\gamma+\delta)}=\frac{p}{\sin(\alpha)}\;\Longleftrightarrow\;c=\frac{p}{\sin(2\gamma+\delta)}\cdot\sin(\alpha)\approx\frac{80\,\text{cm}}{\sin(2\cdot22,85^{\circ}+12,15^{\circ})}\cdot\sin(55^{\circ})\approx77,4\,\text{cm}\,.\)
Der Abstand vom Umkehrpunkt \(\mathrm{U}_{1}\) zur Wand beträgt also ca. 77,4 cm.