Kapitel 7: Satz des Pythagoras und Trigonometrie (S. 93)
Aufgabe 1
Auch wenn es hier um Mathematik geht brauchen wir zunächst ein bisschen Physik; wir brauchen nämlich einen Zusammenhang zwischen dem Gewicht \(m\) und der Dichte \(\varrho\) eines Körpers. Ein Blick in ein schlaues Buch (oder eine dunkle Erinnerung) liefert:
\(\displaystyle\varrho=\frac{m}{V}\;\Longleftrightarrow\;m=\varrho\cdot V\,,\)
wobei \(V\) das Volumen des Körpers ist. Wir müssen also zunächst das Volumen des gefrästen Messingwürfels bestimmen. Dazu ziehen wir einfach das Volumen, dass die beiden Kegelstümpfe haben vom Volumen des gesamten Messingblocks ab. Für das Volumen \(V_{st}\) eines Kegelstumpfes gilt (hier können wir bei Bedarf wieder eine Formelsammlung zu Rate ziehen):
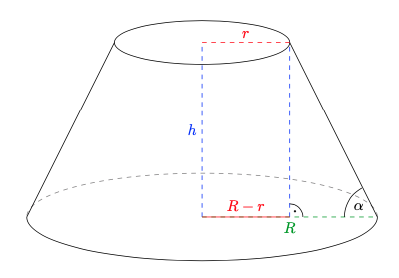
\(V_{st}=\frac{1}{3}\cdot h\cdot\pi\cdot(R^2+r\cdot R+r^2)\)
Aus den gegebenen Daten wissen wir bereits, dass \(R=3\,\text{cm}\) ist. Es fehlt also nur \(r\). Da wir darüber hinaus aber auch die Höhe \(h=4\,\text{cm}\) kennen (der Würfel hat ja eine Seitenlänge von 8 cm), liefert der Tangens
\(\displaystyle\tan(\alpha)=\frac{h}{R-r}\;\Longleftrightarrow\;r=R-\frac{h}{\tan(\alpha)}\,,\)
also
\(r=3\,\text{cm}-\frac{4}{\tan(73^{\circ})}\,\text{cm}\approx1,78\,\text{cm}\,.\)
Damit ist das Volumen des gefrästen Messingwürfels:
\(\begin{align*}V&=V_{W}-2\cdot V_{st}\\&=a^3-\frac{2}{3}\cdot\pi\cdot(R^2+r\cdot R+r^2)\\&=(8\,\text{cm})^3-\frac{2}{3}\cdot4\,\text{cm}\cdot\pi\cdot\big((1,78\,\text{cm})^2+1,78\,\text{cm}\cdot3\,\text{cm}+(3\,\text{cm})^2\big)\approx365,32\,\text{cm}^3\,.\end{align*}\)
Das entspricht einem Gewicht von
\(\displaystyle m=\varrho\cdot V\approx8,3\,\text{g/cm}^3\cdot365,32\,\text{cm}^3\approx3032,16\,\text{g}\approx3,0\,\text{kg}\,.\)
(b) Aus obiger Skizze können wir leicht ablesen, dass für die Länge einer Seitenkante \(a\) gerade
\(\displaystyle\sin(\alpha)=\frac{h}{a}\;\Longleftrightarrow\;a=\frac{h}{\sin(\alpha)}=\frac{4}{\sin(73^{\circ})}\,\text{cm}\approx3,83\,\text{cm}\,.\)
(c) DasVolumen des mit Silber überzogenen Werkstücks \(V_{vs}\) erhalten wir, indem wir das Volumen des um 0,1 mm dickeren Würfels betrachten und davon das Volumen des um 0,2mm dünneren Kegelstumpfes abziehen. Für diesen Kegelstumpf reduziert sich der Radius \(r\) um 0,1 mm und die Höhe \(h\) wird um 0,1mm länger. Damit wird der Radius \(R\) zu
\(\displaystyle R’=r’+\frac{h‘}{\tan(\alpha)}=1,77\,\text{cm}+\frac{4,01}{\tan(73^{\circ})}\,\text{cm}\approx2,996\,\text{cm}\)
Damit ist dann das Volumen der Silberschicht einfach \(V_{s}=V_{vs}-V\).
Für das Volumen des mit silber überzogenen Werkstücks gilt nach obiger Formel gerade
\(\begin{align*}V_{vs}&=(a‘)^3-\frac{2}{3}\cdot h’\cdot\pi\cdot\big((r‘)^2+r’\cdot R’+(R‘)^2\big)\\&=(8,02\,\text{cm})^3-\frac{2}{3}\cdot4,01\,\text{cm}\cdot\pi\cdot\big(1,77\,\text{cm})^2+1,77\,\text{cm}\cdot2,996\,\text{cm}+(2,996\,\text{cm})^2\big)\\&\approx 369,62\,\text{cm}^3\,.\end{align*}\)
Also brauchen wir für den Silberüberzug etwa
\(V_{s}=V_{vs}-V=369,62\,\text{cm}^3-365,32\,\text{cm}^3=4,3\,\text{cm}^3\,,\)
also
\(m_{s}=\varrho_{s}\cdot V_{s}=10,5\,\text{g/cm}^3\cdot 4,3\,\text{cm}^3=45,15\,\text{g}\)
Silber.
Aufgabe 2
Aus dem blauen Dreieck können wir mit dem Tangens die Entfernung \(s\) bis zum Start der Landebahn errechnen. Für diese Strecke gilt gerade
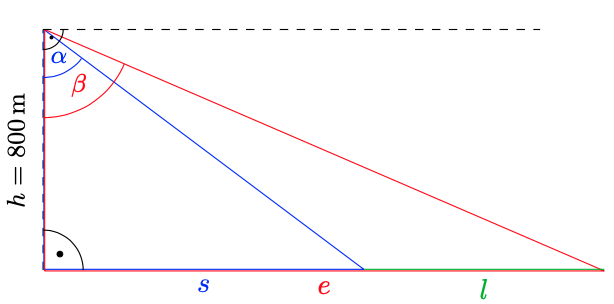
\(\displaystyle\tan(\alpha)=\frac{s}{h}\;\Longleftrightarrow\;s=h\cdot\tan(\alpha)=800\,\text{m}\cdot\tan(57^{\circ})\approx1231,89\,\text{m}\,.\)
Ebenso lässt sich aus dem roten Dreieck die Entfernung \(e\) bis zum Ende der Landebahn berechnen:
\(\displaystyle\tan(\beta)=\frac{e}{h}\;\Longleftrightarrow\;e=h\cdot\tan(\beta)=800\,\text{m}\cdot\tan(70^{\circ})\approx2197,98\,\text{m}\,.\)
Damit hat die Landebahn eine Länge von \(l=e-s=2197,98\,\text{m}-1231,89\,\text{m}=966,09\,\text{m}\,.\)