Kapitel 7: Satz des Pythagoras und Trigonometrie (S. 91)

Aufgabe 1

(a) Da \(\gamma=\frac{\pi}{2}\) liegt hier offensichtlich ein rechtwinkliges Dreieck mit Hypothenuse \(c=18\,\text{cm}\) vor. Damit ist dann zum Beispiel

\(\cos(\beta)=\frac{a}{c}\;\Longleftrightarrow\;a=c\cdot\cos(\beta)=18\,\text{cm}\cdot\cos(51,06^{\circ})\approx11,31\,\text{cm}\)

und

\(\sin(\beta)=\frac{b}{c}\;\Longleftrightarrow\;b=c\cdot\sin(\beta)=18\,\text{cm}\cdot\sin(51,06^{\circ})\approx14\,\text{cm}\,.\)

Schließlich liefert die Innenwinkelsumme, dass

\(\alpha=180^{\circ}-\beta-\gamma=180^{\circ}-51,06^{\circ}-90^{\circ}=38,94^{\circ}\,.\)

(b) Auch dieses Dreieck ist rechtwinklig mit Hypothenuse \(c=10\,\text{cm}\) und somit liefert der Satz des Pythagoras:

\(c^2=a^2+b^2\;\Longleftrightarrow\;b=\sqrt{c^2-a^2}=\sqrt{(10\,\text{cm})^2-(8\,\text{cm})^2}=\sqrt{36\,\text{cm}^2}=6\,\text{cm}\,.\)

Außerdem gilt:

\(\displaystyle\cos(\alpha)=\frac{b}{c}\;\Longleftrightarrow\;\alpha=\arccos\left(\frac{b}{c}\right)=\arccos\left(\frac{8\,\text{cm}}{10\,\text{cm}}\right)\approx 0,2\,\pi\,,\)

sowie

\(\displaystyle\sin(\beta)=\frac{b}{c}\;\Longleftrightarrow\;\beta=\arcsin\left(\frac{b}{c}\right)=\arcsin\left(\frac{8\,\text{cm}}{10\,\text{cm}}\right)\approx 0,3\,\pi\,,\)

\(\displaystyle\gamma=\pi-\alpha-\beta=\pi-\frac{\pi}{6}-\frac{\pi}{4}=\frac{7}{12}\pi\,.\)

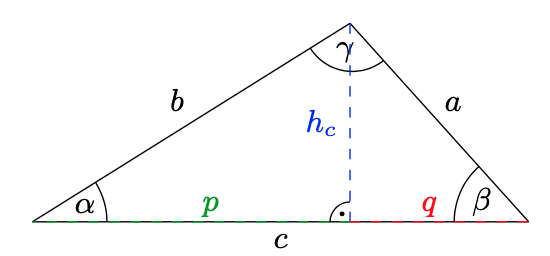
Das Dreieck ist also nicht rechtwinklig und damit wird die Bestimmung der verbliebenen Seitenlängen etwas komplizierter. Wir beginnen mit der Seite a und tragen dazu noch die Höhe \(h_{c}\) in das Dreieck ein. Diese teilt das Dreieck in zwei rechtwinklige Teildreiecke, auf denen wir nun wieder mit Cosinus, Sinus und Tangens arbeiten können.

Dann gilt einerseits \(p+q=c\) und andererseits

\(\begin{alignat*}{3}\displaystyle \cos(\alpha)&=\frac{p}{b}\,,\quad&\sin(\alpha)=\frac{h_{c}}{b}\,,\quad&\tan(\alpha)&=\frac{h_c}{p}\\\cos(\beta)&=\frac{q}{b}\,,\quad&\sin(\beta)=\frac{h_{c}}{b}\,,\quad&\tan(\beta)&=\frac{h_c}{q}\,.\end{alignat*}\)

Nutzen wir nun den Tangens aus folgt, dass

\(\displaystyle c=p+q=\frac{h_{c}}{\tan(\alpha)}+\frac{h_{c}}{\tan(\beta)}=h_{c}\cdot\frac{\tan(\beta)+\tan(\alpha)}{\tan(\alpha)\cdot\tan(\beta)}\,,\)

also

\(\displaystyle h_{c}=c\cdot\frac{\tan(\alpha)\cdot\tan(\beta)}{\tan(\beta)+\tan(\alpha)}=5\,\text{cm}\cdot\frac{\tan\left(\frac{\pi}{6}\right)\tan\left(\frac{\pi}{4}\right)}{\tan\left(\frac{\pi}{4}\right)+\tan\left(\frac{\pi}{6}\right)}=5\,\text{cm}\cdot\frac{1}{1+\sqrt{3}}\approx1,83\,\text{cm}\,.\)

Somit liefert nun der Sinus

\(\begin{align*}\displaystyle a&=\frac{h_{c}}{\sin(\beta)}\approx\frac{1,83}{\sin\left(\frac{\pi}{4}\right)}\,\text{cm}\approx2,59\,\text{cm}\\b&=\frac{h_{c}}{\sin(\alpha)}\approx\frac{1,83}{\sin\left(\frac{\pi}{6}\right)}\,\text{cm}=3,69\,\text{cm}\end{align*}\)

Aufgabe 2

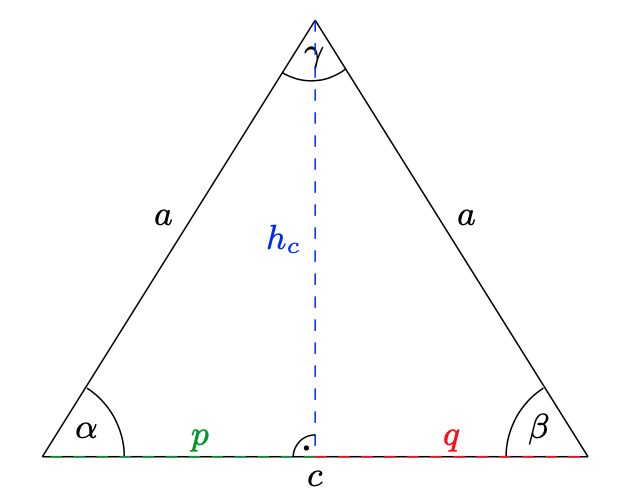
Wie im Beispiel auf Seite 90 teilt die Höhe \(h_{c}\) das Dreieck in zwei deckungsgleiche Teildreiecke. Damit ist also \(\alpha=\beta\) und wegen der Innenwinkelsumme

\(2\alpha=\alpha+\beta=180^{\circ}-\gamma=180^{\circ}-120^{\circ}=60^{\circ}\,,\)

also \(\alpha=\beta=30^{\circ}\). Außerdem teilt die Höhe die Grundseite \(c\) in zwei gleichlange Stücke \(p=q\) und nun liefert der Cosinus

\(\displaystyle \cos(\beta)=\frac{q}{a}\;\Longleftrightarrow\;q=a\cdot\cos(\beta)=6\,\text{cm}\cdot\cos(30^{\circ})=\sqrt{3}\,\text{cm}\approx1,73\,\text{cm}\,.\)

Damit ist dann \(c=p+q=2q=2\sqrt{3}\,\text{cm}\approx3,46\,\text{cm}\,.\)