Kapitel 7: Satz des Pythagoras und Trigonometrie (S. 89)
Aufgabe 1
Mit der Umrechnungsformel von Seite 88 und dem Taschenrechner erhalten wir:
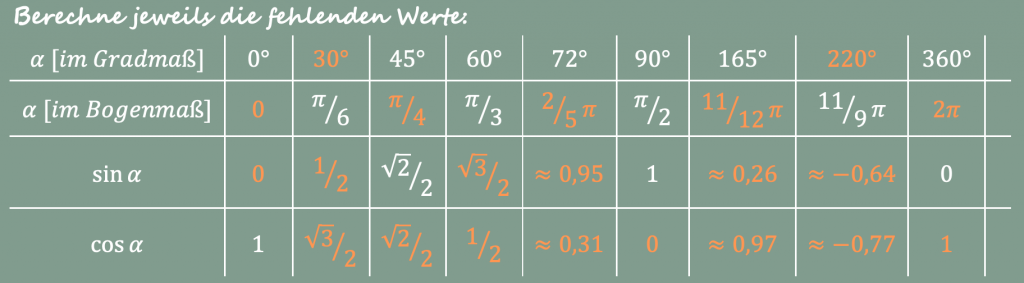
Aufgabe 2
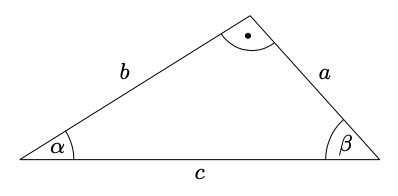
Wie auf Seite 88 beschrieben gelten in dem rechts abgebildeten Dreieck feste Beziehungen zwischen den Katheten, der Hypothenuse und den Winkeln. Zusammen mit dem Satz des Pythagoras reichen die Informationen aus der Aufgabenstellung um die noch fehlenden Größen zu berechnen.
(a) Zwischen den Seiten \(a\) und \(c\) sowie dem Winkel \(\alpha\) gilt die Beziehung
\(\displaystyle \sin(\alpha)=\frac{Gegenkathete}{Hypothenuse}=\frac{a}{c}\,,\)
also
\(\displaystyle c\cdot\sin(\alpha)=a\;\Longleftrightarrow\;c=\frac{a}{\sin(\alpha)}=\frac{5}{\sin(35^{\circ})}\,\text{cm}\approx8,717\,\text{cm}\,.\)
Für die Seite b können wir nun zum Beispiel den Satz des Pythagoras verwenden. Dieser liefert (da Längen stets positiv sind):
\(c^2=a^2+b^2\;\Longleftrightarrow\;b=\sqrt{c^2-a^2}\approx\sqrt{(8,717\,\text{cm})^2-(5\,\text{cm})^2}\approx7,140\,\text{cm}\,.\)
Ein kleiner Nachteil an diesem Rechenweg liegt in der Tatsache, dass wir \(b\) mit einem bereits gerundeten (also ungenauen Wert) für \(c\) berechnen. Das „verschlimmert“ natürlich den Rundungsfehler, allerdings in der Regel nur so minimal, dass es praktisch kaum relevant ist. Alternativ könnte man natürlich auch einfach auf den Tangens zurückgreifen, denn schließlich ist
\(\displaystyle \tan(\alpha)=\frac{Gegenkathete}{Ankathete}=\frac{a}{b}\;\Longleftrightarrow\;b=\frac{a}{\tan(\alpha)}\,.\)
Dann folgt:
\(\displaystyle b=\frac{a}{\tan(\alpha)}=\frac{5}{\tan(35^{\circ})}\,\text{cm}\approx7,141\,\text{cm}\,,\)
die Werte unterscheiden sich also tatsächlich erst in der dritten Nachkommastelle. Schließlich bleibt noch der Winkel \(\beta\), den wir einfach über die Innenwinkelsumme eines Dreiecks erhalten. Es gilt nämlich in jedem Dreieck, dass die Summe aller Winkel gerade \(180^{\circ}=\pi\) ist. Entsprechend ist klar, dass:
\(\beta=180^{\circ}-90^{\circ}-\alpha=90^{\circ}-35^{\circ}=55^{\circ}\,.\)
Natürlich hätte man den Winkel \(\beta\) auch vorher schon ausrechnen und mit diesem die Seiten \(b\) und \(c\) bestimmen können.
(b) Da hier im Gegensatz zu Aufgabenteil (a) die Seite \(b\) gegeben ist, arbeiten wir hier mit dem Kosinus. Es ist:
\(\displaystyle\cos(\alpha)=\frac{Ankathete}{Hypothenuse}=\frac{b}{c}\;\Longleftrightarrow\;c=\frac{b}{\cos(\alpha)}\,,\)
also
\(\displaystyle c=\frac{b}{\cos(\alpha)}=\frac{10}{\cos(0,31\pi)}\,\text{cm}=17,79\,\text{cm}\,.\)
Benutzen wir zudem den Tangens, folgt
\(\displaystyle \tan(\alpha)=\frac{a}{b}\;\Longleftrightarrow\;a=b\cdot\tan(\alpha)=10\,\text{cm}\cdot\tan(0,31\pi)\approx14,71\,\text{cm}\,,\)
und mit der Innenwinkelsumme ist:
\(\displaystyle \beta=\pi-\frac{\pi}{2}-\alpha=\frac{\pi}{2}-0,31\pi=0,19\pi\,.\)
(c) In dem rechtwinkligen Dreieck gilt:
\(\displaystyle\cos(\beta)=\frac{b}{c}\qquad\text{und}\qquad\sin(\beta)=\frac{a}{c}\,,\)
also
\(\begin{align*}&b=\cos(\beta)\cdot c=\cos\left(\frac{\pi}{3}\right)\cdot4\,\text{cm}=2\,\text{cm}\,,\\&a=\sin(\beta)\cdot c=\sin\left(\frac{\pi}{3}\right)\cdot 4\,\text{cm}=2\sqrt{3}\,\text{cm}\approx2,88\,\text{cm}\,.\end{align*}\)
Wieder liefert die Innenwinkelsumme
\(\displaystyle\alpha=\pi-\frac{\pi}{2}-\beta=\frac{\pi}{2}-\frac{\pi}{3}=\frac{\pi}{6}\,.\)