Kapitel 7: Satz des Pythagoras und Trigonometrie (S. 87)
Aufgabe 1
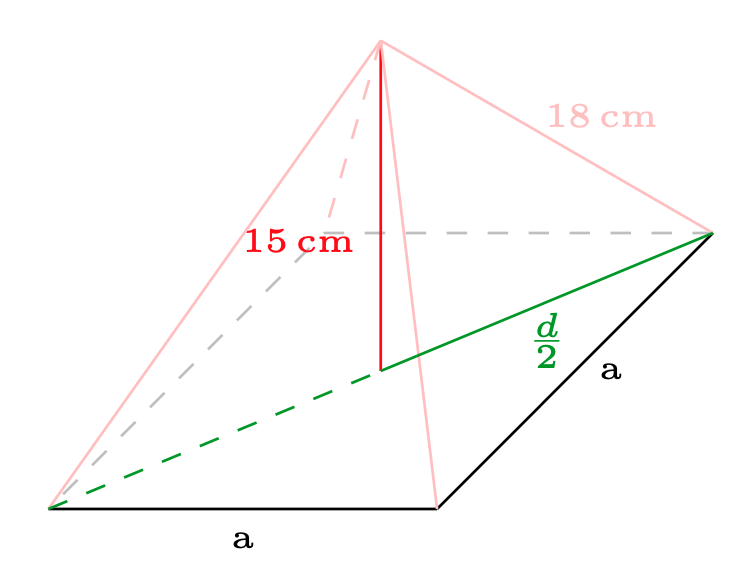
(a) Da die Höhe zusammen mit einer Seitenkante und der Diagonalen der Grundfläche ein rechtwinkliges Dreieck bildet, gilt auch hier der Satz des Pythagoras. Dabei liegt die Seitenkante dem rechten Winkel gegenüber, es gilt also
\(\begin{align*}&\hspace{-0.5cm}(18\,\text{cm})^2=\left(\frac{d}{2}\right)^2+(15\,\text{cm})^2\\&\;\Longleftrightarrow\;\left(\frac{d}{2}\right)^2=324\,\text{cm}^2-225\,\text{cm}^2=99\,\text{cm}^2\,,\end{align*}\)
d.h. (Längen sind positiv!)
\(d=2\sqrt{99}\,\text{cm}=6\sqrt{11}\,\text{cm}\).
Auch in der quadratischen Grundfläche ist die Diagonale Hypothenuse eines rechtwinkligen Dreiecks, dessen beiden Katheten gerade gleich lang sind. Entsprechend liefert der Satz des Pythagoras hier nun gerade (Beachte, dass eine Länge immer positiv ist!):
\(\begin{align*}d^2=a^2+a^2=2a^2\;\Longleftrightarrow\;a=\frac{d}{\sqrt{2}}=3\sqrt{22}\,\text{cm}\approx14,07\,\text{cm}\,.\end{align*}\)
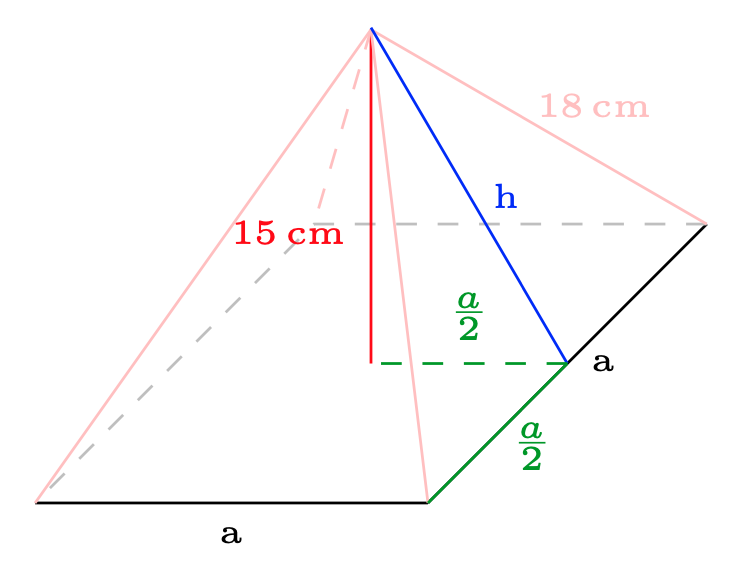
(b) Die dreieckigen Seitenflächen sind gleichschenklige Dreiecke, deren Höhe die Grundseite, also die Seite a, gerade halbiert. Darüber hinaus bildet die Höhe h der Seitenfläche zusammen mit der Seitenkante und der halbierten Grundseite \(\frac{a}{2}\) ein rechtwinkliges Dreieck in dem die Seitenkante der Hypothenuse entspricht. Der Satz des Pythagoras liefert also (Längen sind positiv!):
\(\begin{align*}&\hspace{-0.5cm}(18\,\text{cm})^2=\left(\frac{a}{2}\right)^2+h^2\\&\;\Longleftrightarrow\;h=\sqrt{324\,\text{cm}^2-\frac{a^2}{4}}=\sqrt{324\,\text{cm}^2-\frac{99}{2}\,\text{cm}^2}=\sqrt{274,5}\,\text{cm}\approx16,57\,\text{cm}\,.\end{align*}\)
Alternativ kann man den Satz des Pythagoras auch auf das rechtwinklige Dreieck, dass durch h, die Höhe der Pyramide und die halbe Breite der Pyramide gebildet wird anwenden. Hier ist h sogar die Hypothenuse und es folgt:
\(\begin{align*}h^2=\left(\frac{a}{2}\right)^2+(15\,\text{cm})^2\;\Longleftrightarrow\;h=\sqrt{\frac{a^2}{4}+225\,\text{cm}^2}=\sqrt{274,5}\,\text{cm}\approx16,57\,\text{cm}\,.\end{align*}\)
(c) Für die Mantelfläche M müssen wir die Seitenflächen S und die Bodenfläche B bestimmen. Da der Flächeninhalt eines Dreieckes gerade [Latex]\frac{1}{2}\cdot g\cdot h[/Latex] (h: Höhe, g: zur Höhe gehörende Grundseite) ist, folgt entsprechend
\(\begin{align*}M&=4\cdot S+B\\&=4\cdot \frac{1}{2}\cdot a\cdot h+a^2\\&=2\cdot a\cdot h+a^2\\&=2\cdot3\sqrt{22}\,\text{cm}\cdot\sqrt{274,5}\,\text{cm}+\left(3\sqrt{22}\,\text{cm}\right)^2\\&=18\sqrt{671}\,\text{cm}^2+198\,\text{cm}^2\approx664,27\,\text{cm}^2\,.\end{align*}\)
Aufgabe 2
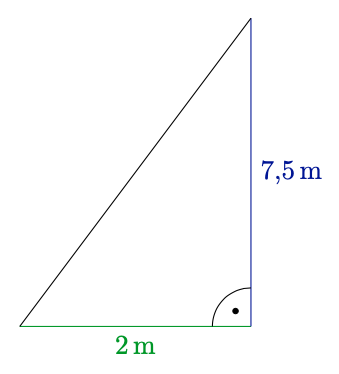
Mit dem Satz von Pythagoras erhalten wir für die gesuchte Länge l:
\(\begin{align*}&\hspace{-0.5cm}l^2=(2\,\text{m})^2+(7,5\,\text{m})^2=60,25\,\text{m}^2\\&\;\Longleftrightarrow\;l=\sqrt{60,25}\,\text{m}\approx7,76\,\text{m}\,.\end{align*}\)