Kapitel 4: Variablen, Terme, Rechengesetze (S. 49)

Aufgabe 1

(a) \( 2x^2\cdot (x+3x)=2x^2\cdot x + 2x^2 \cdot 3x = 2x^3+6x^3= 8x^3\).

Im ersten Schritt wurde das Distributivgesetz verwendet. Eine Lösung ist aber auch ohne dieses möglich, z. B. so: \(2x^2\cdot(x+3x)=2x^2 \cdot 4x=8x^3\).

(b) \( 0,231 \cdot 2 \cdot 7 \cdot \frac{1}{7} = (0,231 \cdot 2) \cdot (7 \cdot \frac{1}{7})=0,462\cdot 1=0,462\)

Hier wurde das Assoziativgesetz zum Setzen der Klammern verwendet.

Hier wurde das Kommutativgesetz zum Tauschen von \( yx \) zu \( xy \) genutzt.

(d) \( 3x+(7x\cdot 2y) = 3x+ 7x\cdot 2y = 3x + 14xy\)

Die Klammer ist hier eigentlich gar nicht notwendig, da die Punktrechnung sowieso Vorfahrt hat. Hier wurde keines der drei Gesetze angewendet.

(e) \( 4c+7d+2c – 8d = 4c + 2c + 7d -8d = 6c – 1d = 6c -d\)

Hier haben wir das Kommutativgesetz für + benutzt.

(f)

\( \begin{align*}2i(3j+3k(2i+2j)) &= 2i\cdot 3j + 2i\cdot 3k(2i+2j)\\ &= 6ij + 6ik(2i+2j)\\ &= 6ij + 6ik\cdot 2i+6ik\cdot 2j\\ &= 6ij + 12i^2k+12ijk\end{align*}\)

Hier wurde im ersten und dritten Schritt jeweils das Distributivgesetz genutzt. Im Buch ist hier außerdem ein kleiner Fehler: Natürlich muss die Klammer am Ende zweimal zugemacht werden.

Aufgabe 2

Das Kommutativgesetz für + kannst du dir z. B. so vorstellen:

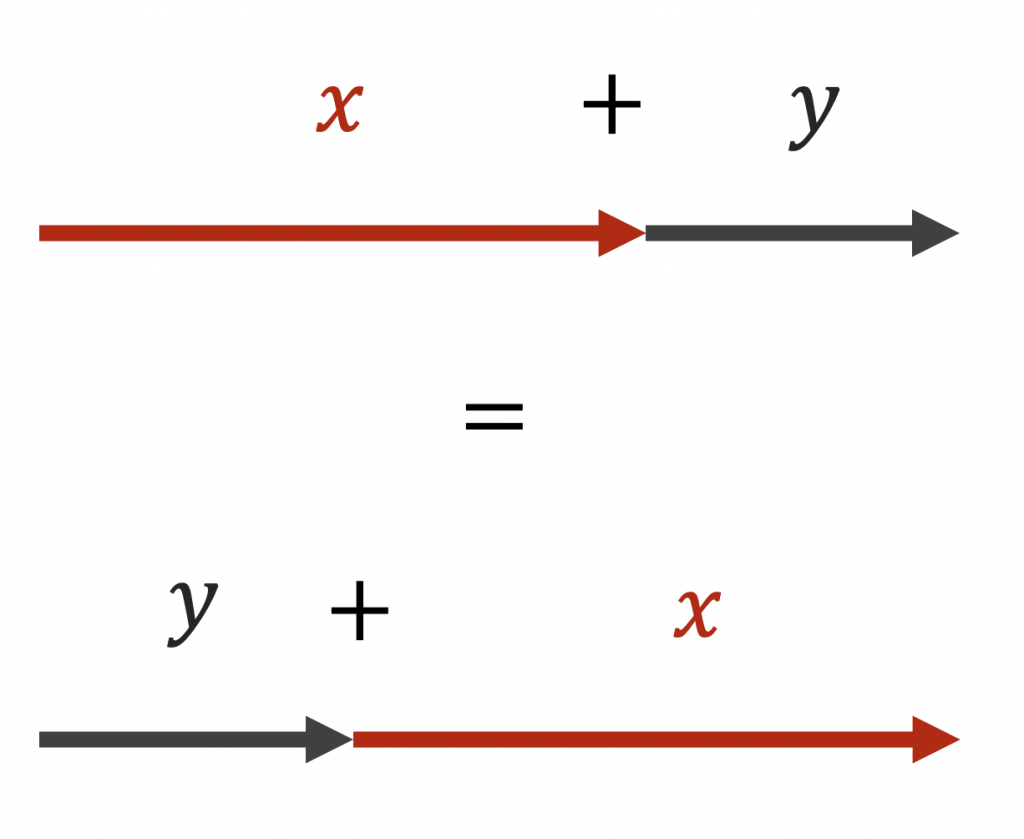
Wenn du zwei Längen \(x\) und \(y\) hast, ist es egal, ob du \(x+y\) oder \(y+x\) berechnest.

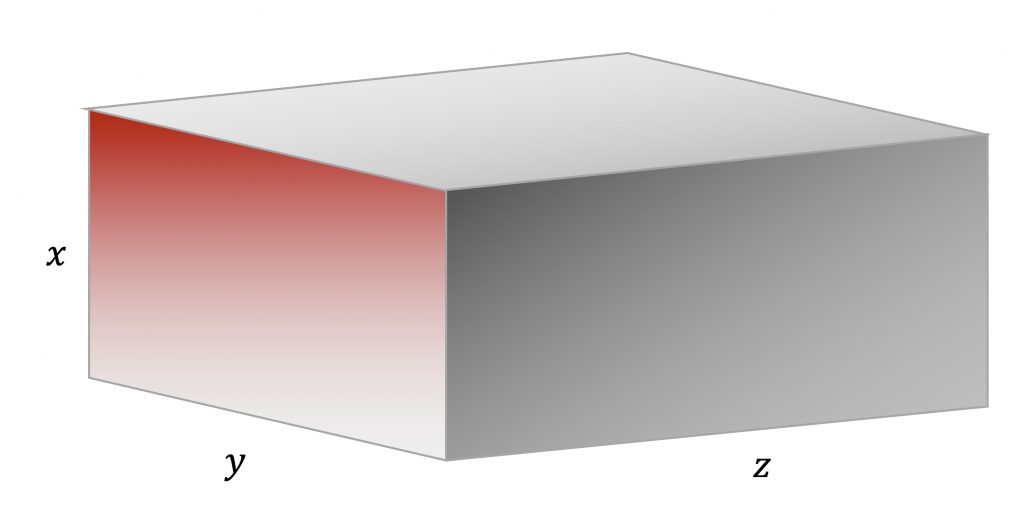
Das Assoziativgesetz für \(\cdot\) kannst du dir z. B. als Volumenberechnung eines Quaders vorstellen: Hier ist es egal, ob du erst die rote Seitenfläche mit den Kanten \(x\) und \(y\) und dann mit der Tiefe \(z\) multiplizierst oder ob du erst die graue Seitenfläche mit den Kanten \(x\) und \(z\) berechnest und dann mit der Breite \(y\) multiplizierst. Du kannst also das Volumen \(V\) als \(V = (x\cdot y)\cdot z\) oder \(V = x\cdot (y\cdot z)\) bestimmen.