Kapitel 3: Ein Blick in die Wahrscheinlichkeitsrechnung (S. 40)

Aufgabe 1

Werfen wir einen Würfel gibt es grundsätzlich sechs mögliche Ergebnisse, nämlich gerade die Augenzahlen 1,2,3,4,5,6. Damit ergibt sich für die Wahrscheinlichkeit der gefragten Ereignisse E:

(a) \(E=\text{„Würfel zeigt Augenzahl drei“}=\{3\}\), also \( \displaystyle P(E)=\frac{1}{6}\approx16,7\%\)

(b) \(E=\text{„Würfel zeigt eine gerade Augenzahl“}=\{2,4,6\}\), also \( \displaystyle P(E)=\frac{3}{6}=\frac{1}{2}=50\%\)

(c) \(E=\text{„Würfel zeigt Augenzahl größer als zwei“}=\{3,4,5,6\}\), also \( \displaystyle P(E)=\frac{4}{6}=\frac{2}{3}=\approx66,7\%\)

(d) \(E=\text{„Würfel zeigt Augenzahl kleiner oder gleich fünf“}=\{1,2,3,4,5\}\), also \( \displaystyle P(E)=\frac{5}{6}\approx83,3\%\)

Aufgabe 2

Übertragen wir die Situation auf das Urnenmodell, ist die Anzahl der möglichen Kombinationen gesucht, aus einer Urne mit sechs Kugeln vier Kugeln ohne Zurücklegen und mit Beachtung der Reihenfolge ( die Farbkombination „rot, gelb, blau, rot“ ist eine andere als „rot, rot, gelb, blau“ zu ziehen ) zu ziehen. Mit unseren Formeln von Seite 37 sind das gerade \(\displaystyle 4!\cdot\left(\begin{array}{c}6\\4\end{array}\right)=\frac{6!}{2!}=6\cdot5\cdot4\cdot3=360\) mögliche Kombinationen. Erlauben wir sogar das Zurücklegen, sind es sogar \(6^4=1296.\)

Aufgabe 3

(a) Das Einstellen des Fahrradschlosses entspricht dem dreimaligen Ziehen aus einer Urne mit 6 Kugeln mit Zurücklegen (auf jedem Rad lässt sich auch dieselbe Zahl einstellen) und Beachtung der Reihenfolge (die Kombination „1,1,2“ ist eine andere als „2,1,1“). Das sind nach unserer Tabelle von Seite 37 gerade \(6^3=216\) mögliche Kombinationen.

(b) Der Dieb weiß also, dass an erster bzw. letzter Stelle nur die Zahlen „2,4,6“, in der Mitte immer noch alle Ziffern möglich sind. Mit dem Produktsatz der Kombinatorik gibt es somit immer noch \(3\cdot6\cdot3=54\) mögliche Kombinationen. Damit ist die Wahrscheinlichkeit, dass er die richtige Kombination errät, gerade \(\displaystyle P=\frac{1}{54}\approx1,9\%.\)

Aufgabe 4

(a) Übertragen auf das Urnenmodell geht es bei der Aufgabe darum fünfmal eine Kugel (die Schalterstellung) aus einer Urne mit zwei Kugeln („an“ und „aus“) zu ziehen. Dabei wird die gezogene Kugel zurückgelegt (es können zwei oder mehr Lampen gleichzeitig an bzw. aus sein) und auf die Reihenfolge geachtet (da jeder Schalter eine andere Farbe schaltet). Es gibt also \(2^5=32\) verschiedene Lichtkonzepte (sofern man „alle Lampen aus“ auch als Lichtkonzept versteht).

(b) Soll die Schwarzlichtlampe brennen, reduziert sich unsere Aufgabe darauf viermal eine Kugel aus der Urne zu ziehen. Dafür gibt es \( 2^4=16\) mögliche Kombinationen. Die Wahrscheinlichkeit, dass bei einer zufällig eingestellten Beleuchtung auch das Schwarzlicht brennt, ist daher \(\displaystyle P=\frac{16}{32}=50\%.\)

Schließen wir den Fall, dass keine Lampe brennt als Lichtkonzept aus, steigt die Wahrscheinlichkeit auf \( \displaystyle P=\frac{16}{32-1}=\frac{16}{31}\approx 51,6\%.\)

Aufgabe 5

Aus der Lostrommel mit acht Losen wird dreimal ohne Zurücklegen und mit Beachtung der Reihenfolge gezogen. Dazu gibt es insgesamt (Seite 37 im Mathebuddy) \(\displaystyle3!\left(\begin{array}{c}8\\3\end{array}\right)=\frac{8!}{5!}=8\cdot7\cdot6=336\) Möglichkeiten. Da nur zwei Kombinationen zum Glück führen, liegt die Gewinnwahrscheinlichkeit bei \(\displaystyle P=\frac{2}{336}=\frac{1}{118}\approx 0,8\%.\)

Aufgabe 6

Zunächst einmal überlegen wir uns wieviele Möglichkeiten es gibt sechs der 49 Zahlen anzukreuzen und zusätzlich eine Superzahl zu wählen. Da jede Zahl nur ein einziges Mal vorkommt (also ohne Zurücklegen) und die Reihenfolge nicht beachtet werden muss (in welcher Reihenfolge die sechs Zahlen angekreuzt werden ist ja egal) gibt es dazu \(\left(\begin{array}{c}49\\6\end{array}\right)=13.983.816 \) und für die Wahl der Superzahl eben gerade 10 Möglichkeiten. Insgesamt gibt es daher \(10\cdot 13.983.816=139.838.160\approx140\)Mio.

(a) Für die vier Richtigen müssen wir aus den tatsächlichen sechs richtigen Zahlen gerade vier auswählen. Das entspricht \(\left(\begin{array}{c}6\\4\end{array}\right)=15\) Möglichkeiten. Insgesamt müssen für einen gültigen Lottoschein aber sechs Zahlen angekreuzt werden und zusätzlich soll die Superzahl falsch sein. Das bedeutet es müssen auch zwei der 43 falschen Zahlen angekreuzt und eine der 9 falschen Superzahlen ausgewählt werden. Dazu gibt es gerade \( \left(\begin{array}{c}43\\2\end{array}\right)=903\) bzw. 9 Möglichkeiten, insgesamt also \(15\cdot903\cdot9=121.905\) Kombinationen um nur vier Richtige anzukreuzen. das entspricht einer Wahrscheinlichkeit von \(\displaystyle P=\frac{121.905}{139.838.160}\approx0,09\%.\)

(b) Da sechs Richtige und zusätzlich die richtige Superzahl nur in einem Fall auftreten können, ist die Wahrscheinlichkeit für dieses Ereignis gerade \(\displaystyle P=\frac{1}{139.838.160}\approx1:140\,\text{Mio}\).

Aufgabe 7

Da Max in jedem Wurf die Augenzahlen 1 bis 6 werfen kann und die Augenzahlen der Reihenfolge nach zusammensetzt, entspricht die Situation im Urnenmodell dem viermaligen Ziehen einer Kugel mit Zurücklegen und Beachtung der Reihenfolge gibt es insgesamt gerade \(6^4=1296\) mögliche Zahlen. Damit er bei seinem Experiment eine Zahl würfelt die größer als 4351 ist muss entweder

Fall 1: beim ersten Wurf eine Augenzahl größer als 4 rauskommen, Ist dies der Fall, kann er in den anderen drei Würfen jede beliebige Augenzahl werfen, hat also hier \(2\cdot6\cdot6\cdot6=432\) Möglichkeiten.

Fall 2: beim ersten Wurf eine 4 und beim zweiten, dritten oder vierten Wurf eine Augenzahl größer als 3,5 oder 1 werfen.

Im zweiten Fall muss er nun im zweiten Wurf entweder eine Zahl größer als 3 werfen oder er wirft eine drei und muss sich dann im dritten oder vierten Wurf steigern.

Fall 2a: Er wirft 4,5 oder 6. Dann sind der dritte und vierte Wurf egal und wir erhalten \(3\cdot6\cdot6=108\) Möglichkeiten.

Fall 2b: Er wirft eine drei. Dann kann er im dritten Wurf entweder eine 6 werfen, so dass der vierte Wurf wieder beliebig sein darf (entspricht 6 Möglichkeiten) oder aber er wirft eine 5. In diesem Fall muss er im letzten Wurf definitiv eine Zahl größer als 1 werfen, was noch einmal 5 Möglichkeiten liefert.

Insgesamt gibt es also \(432+108+6+5=551\) mögliche Kombinationen für eine größere Zahl. Das entspricht einer Wahrscheinlichkeit von \(\displaystyle P=\frac{551}{1296}\approx42,5\%\).

Aufgabe 8

Da zwei der fünf Sektoren einem Treffer entsprechen ist die Trefferwahrscheinlichkeit gerade \(P(T)=\frac{2}{5}=40% \) und die Wahrscheinlichkeit für eine Niete somit \(P(N)=P(T)\)\(=1-P(T)=\)\(60\%.\) Drehen wir nun viermal, ergibt sich das nachfolgende Baumdiagramm:

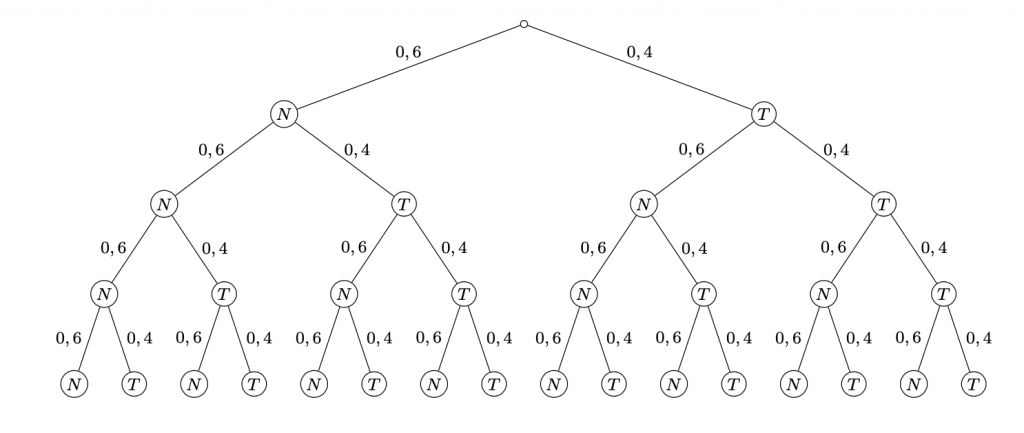
(a) Genau zwei Treffer erhalten wir in sechs der 16 Baumäste. Jeder dieser Äste hat eine Wahrscheinlichkeit von \(P_{\text{Ast}}=0,4^2\cdot 0,6^2=0,0576=5,76\%\text{ (2mal Treffer, 2mal Niete)}\), so dass wir insgesamt eine Wahrscheinlichkeit von \( P=6\cdot5,76\%=34,56\%\) für genau zwei Treffer erhalten.

(b) Keinen Treffer erhalten wir nur, wenn wir viermal eine Niete treffen. Das entspricht nur dem ganz linken Ast in unserem Diagramm und daher erhalten wir keinen Treffer mit einer Wahrscheinlichkeit von \(P=0,6^4=0,1296=12,96\%\,.\)

(c) Weniger als eine Niete bedeutet nichts anderes, als dass wir bei viermal Drehen keine Niete erwischen. Das entspricht in unserem Baumdiagramm gerade dem ganz rechten Ast, tritt also mit einer Wahrscheinlichkeit von \(P=0,4^4=0,0256=2,56\%\) ein.

(d) Mehr als zwei Treffer erhalten wir wenn wir entweder drei oder sogar vier Treffer hinbekommen. Die Wahrscheinlichkeit von vier Treffern haben wir bereits in (c) berechnet: \(P_{4T}=2,56\%\) Drei Treffer erhalten wir in vier weiteren Baumästen, deren Wahrscheinlichkeit jeweils \(P_{\text{Ast}}=0,4^3\cdot 0,6^1\)\(=0,0384\)\(=3,84\%\text{ (3mal Treffer, 1mal Niete)}\) ist. Also ist die Wahrscheinlichkeit für mehr als zwei Treffer: \(P=4\cdot P_{\text{Ast}}+P_{4T}\)\(=4\cdot3,84\%+2,56\%\)\(=17,92\%\,.\)

Alternativ kann man hier statt eines Baumdiagramms auch mit den Formeln der Kombinatorik arbeiten. Betrachten wir zum Beispiel Teilaufgabe (a), können wir uns alternativ zunächst überlegen, dass bei vierfachem Drehen jedes Ergebnis, dass genau zwei Treffer enthält, die gleiche Wahrscheinlichkeit hat: \(P_{2T}=0,4^2\cdot0,6^2\)\(=0,0576=5,76\%\). Jetzt müssen wir uns nur noch überlegen, wieviele solcher Ergebnisse mit genau zwei Treffern es gibt. Das entspricht aber gerade der Frage danach aus den vier Drehrunden, zwei auszuwählen, in denen wir die Treffer setzen. Das geschieht ohne Zurücklegen (eine gespielte Runde können wir nicht nochmal spielen) und ohne Beachtung der Reihenfolge (in welcher Runde wir treffen ist egal). Es gibt also \(\left(\begin{array}{c}4\\2\end{array}\right)=6\) Möglichkeiten und wir erhalten als Wahrscheinlichkeit für genau zwei Treffer: \(P=6\cdot5,76\%\)\(=34,56\%\). Entsprechend erhalten wir mit diesem Ansatz in (d):

\(P=P_{\text{3 Treffer}}+P_{\text{4 Treffer}}\)\(=\left(\begin{array}{c}4\\3\end{array}\right)\cdot0,4^3\cdot0,6+\left(\begin{array}{c}4\\4\end{array}\right)\cdot0,4^4\)\(=17,92\%\)