Kapitel 3: Ein Blick in die Wahrscheinlichkeitsrechnung (S. 39)
Aufgabe 1
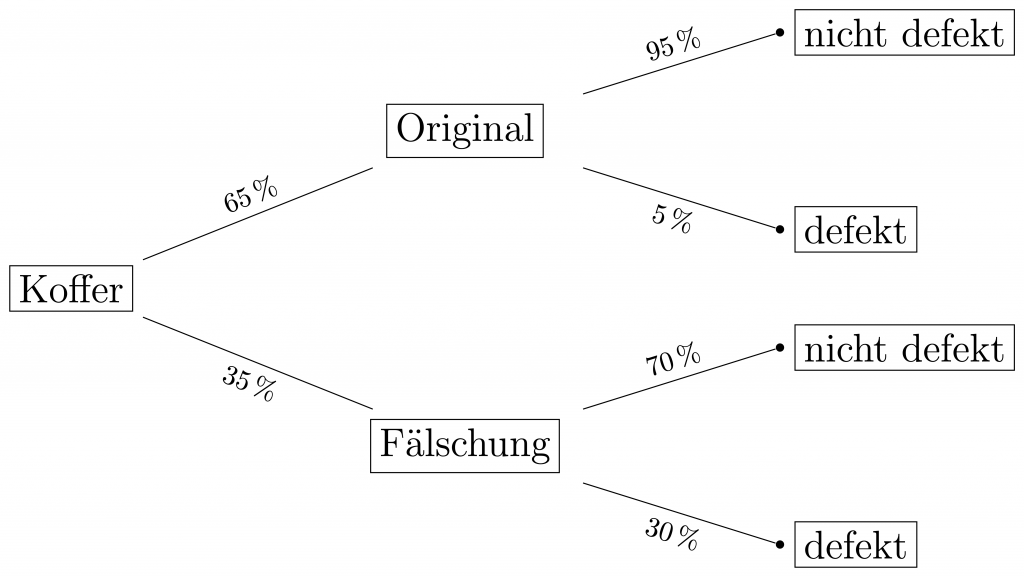
(a) In dem links abgebildeten Baumdiagramm entspricht die gesuchte Wahrscheinlichkeit gerade dem obersten Pfad. Daher ist:
\(\displaystyle P=65\,\%\cdot5\,\%=\frac{65}{100}\cdot\frac{5}{100}=\frac{325}{10000}=3,25\,\%\)(b) Für eine funktionierende Uhr müssen wir die Wahrscheinlichkeit der beiden Pfade die zu einer nicht defekten Uhr führen addieren. Wir erhalten:
\( P=65\,\%\cdot95\,\%+35\,\%\cdot70\,\%=86,25\,\% \)Aufgabe 2
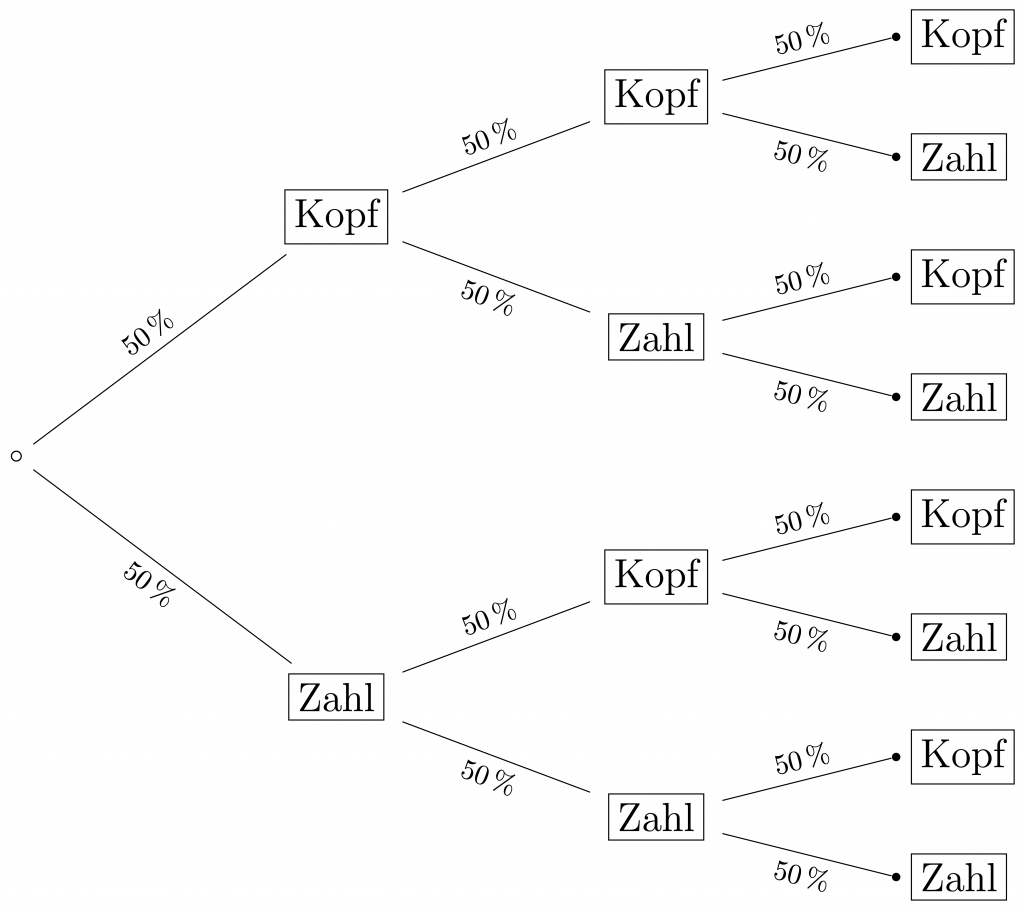
Die Wahrscheinlichkeit bei drei Münzwürfen mindestens zweimal Zahl zu werfen entspricht, erhalten wir indem wir im rechts abgebildeten Baumdiagramm alle Pfade mit zwei oder mehr „Zahl“-Ergebnissen addieren:
\(\begin{align*}P=\,&P(\,\text{Zahl},\,\text{Zahl},\,\text{Zahl}\,)+P(\,\text{Zahl},\,\text{Zahl},\,\text{Kopf}\,)\\+&P(\,\text{Zahl},\,\text{Kopf},\,\text{Zahl}\,)+P(\,\text{Kopf},\,\text{Zahl},\,\text{Zahl}\,)\\=\,&4\cdot50\%\cdot50\%\cdot50\%\\=\,&50\%\end{align*}\)Damit ist das Ereignis mindestens zweimal Zahl zu werfen genauso wahrscheinlich wie das Gegenereignis (höchstens einmal Zahl zu werfen). Sofern wir also gerade in „Zockerlaune“ sind steht einem Spielchen nichts im Wege: DEAL !