Kapitel 2: Prozent- und Zinsrechnung (S. 27)
Aufgabe 1

Die Werte der Tabelle lassen sich alle mit der Grundgleichung für Prozentwerte \(W=G\cdot p\) berechnen:
\(\displaystyle(1)\;W=G\cdot p=80\cdot\frac{62,5}{100}=50\) \(\displaystyle(2)\;W=G\cdot p\;\Longleftrightarrow\;p=\frac{W}{G}=\frac{66,5}{152}=0,4375=43,75\,\% \) \(\displaystyle(3)\;W=G\cdot p\;\Longleftrightarrow\;G=\frac{W}{p}=\frac{316,5}{0,3}=1055 \) \(\displaystyle(4)\;W=G\cdot p=0,016\cdot\frac{75}{100}=0,012\) \(\displaystyle(5)\;W=G\cdot p\;\Longleftrightarrow\;p=\frac{W}{G}=\frac{0,425}{2,125}=0,2=20\,\%\) \(\displaystyle(6)\;W=G\cdot p\;\Longleftrightarrow\;G=\frac{W}{p}=\frac{0,432}{0,45}=0,96\)Aufgabe 2
(a) Da die Fahrtkosten mit \(94\,€\) einem Prozentsatz von \(p=12\,\%\) entsprechen, gaben Studierende 2016 im Schnitt
\(\displaystyle G=\frac{W}{p}=\frac{94\,€}{0,12}\approx783,33\,€\)
im Monat aus.
(b) Um bei der Berechnung nicht auf den gerundeten Grundwert aus (a) zurückzugreifen, können wir hier gut mit einem Dreisatz arbeiten:
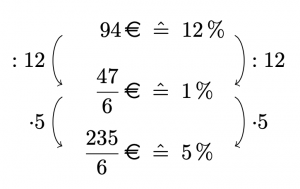
Damit haben Studierende 2016 ca. \(\frac{235}{6}\,€\approx39,17\,€\) für Kleidung ausgegeben.
(c) Abzüglich der anderen Kosten bleiben für die Miete im Schnitt \(39\,\%\) übrig. Wieder liefert ein Dreisatz:
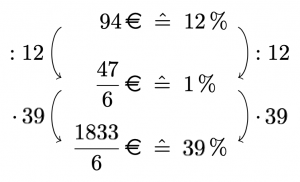
Also haben Studierende im Jahr 2016 ca. \(\frac{1833}{6}\,€=305,50\,€\) für Miete ausgegeben.
(d) Da das Kreissegment für Ernährung \(21\,\%\) des gesamten Kreises entspricht, entspricht der zugehörige Mittelpunktswinkel \(\alpha\) auch\(21\,\%\) des Mittelpunktwinkels eines Vollkreises. Das entspricht gerade:
\(\displaystyle \alpha=360^{\circ}\cdot\frac{21}{100}=75,6^{\circ}\,.\)
Aufgabe 3
(a) Da sich von den \(61,69\,\text{Mio.}\) wahlberechtigten Menschen ungefähr \(46,98\,\text{Mio.}\) an der Wahl beteiligt haben, entspricht das einem Prozentsatz von
\(\displaystyle p=\frac{W}{G}=\frac{46,98\,\text{Mio.}}{61,69\,\text{Mio.}}\approx0,7615=76,15\,\%\,.\)
(b) Da sich die \(1,43\,\text{Mio.}\) 18- bis 20-Jährigen einem Prozentsatz von \(69,9\,\%\) entsprechen, erhalten wir für den zugehörigen Grundwert:
\(\displaystyle G=\frac{W}{p}=\frac{1,43\,\text{Mio.}}{0,699}\approx2,05\,\text{Mio.}\)
Es waren also etwa \(2,05\,\text{Mio.}\) der 18- bis 20-Jährigen wahlberechtigt.
Aufgabe 4

Die Werte der Tabelle lassen sich direkt durch Umstellen der Formel \(W=G\cdot(1+p)\) (Vermehrung) bzw. \(W=G\cdot(1-p)\) (Verminderung) berechnen. Bei diesen Formeln wird grundsätzlich mit dem positiven Prozentsatz \(p\) gerechnet. Das Vorzeichen, das in der Tabelle angibt, ob es sich um eine Vermehrung oder Verminderung handelt, wird durch die Auswahl der passenden Formel berücksichtigt.
(1) Vermehrung: \(\;W=G\cdot(1+p)=15\cdot\left(1+\frac{19}{100}\right)=17,85\)
(2) Vermehrung: \(\;W=G\cdot(1+p)\;\Longleftrightarrow\;p=\frac{W}{G}-1=\frac{0,6}{0,48}-1=\frac{1}{4}=\frac{25}{100}=25\,\%\)
(3) Vermehrung: \(\;W=G\cdot(1+p)\;\Longleftrightarrow\;G=\frac{W}{1+p}=\frac{169}{1+0,3}=130\)
(4) Verminderung: \(\;W=G\cdot(1-p)=96\cdot\left(1-\frac{12,5}{100}\right)=84\)
(5) Verminderung: \(\;W=G\cdot(1-p)\;\Longleftrightarrow\;p=1-\frac{W}{G}=1-\frac{11,15}{44,6}=\frac{3}{4}=\frac{75}{100}=75\,\%\), also \(-75\,\%\) als Tabelleneintrag
(6) Verminderung: \(\;W=G\cdot(1-p)\;\Longleftrightarrow\;G=\frac{W}{1-p}=\frac{88,11}{1-0,11}=99\)
Aufgabe 5
Nennen wir den Aktienkurs zu Beginn \(K_{0}\), erhalten wir für den Kurs nach drei Jahren:
\(K_{3}=\left[\left(K_{0}\cdot(1+0,2)\right)\cdot(1+0,2)\right]\cdot(1+0,2)=K_{0}\cdot1,02^3=K_{0}\cdot1,061208\,.\)
Für den prozentualen Zuwachs p in diesen drei Jahren erhalten wir damit
\(\displaystyle K_{3}=K_{0}\cdot(1+p)\;\Longleftrightarrow\;p=\frac{K_{3}}{K_{0}}-1=1,061208-1=0,061208\approx6,12\,\%\,.\)
Aufgabe 6
Für den Zinssatz p erhalten wir
\(\displaystyle K_{1}=K_{0}\cdot(1+p)\;\Longleftrightarrow\;p=\frac{K_{1}}{K_{0}}-1=\frac{1272,11\,€}{1190\,€}-1=0,069=6,9\,\%\,.\)
Das Möbelgeschäft verlangt also einen Zinssatz von \(6,9\,\%.\)