Kapitel 2: Prozent- und Zinsrechnung (S. 25)

Aufgabe 1

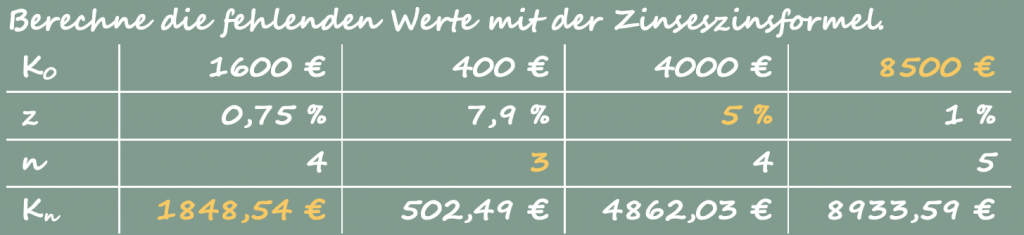
Mit der Zinseszins-Formel \(K_{n}=K_{0}\cdot(1+p)^n\) folgt

\(\displaystyle(1)\;K_{4}=1600\,€\cdot\left(1+\frac{0,75}{100}\right)^4\approx1648,54\,€\\[11pt]\) \(\begin{align*}\displaystyle(2)\;K_{n}=K_{0}\cdot(1+p)^n\;&\Longleftrightarrow\;\ln\left(\frac{K_{n}}{K_{0}}\right)=n\cdot\ln(1+p)\\&\Longleftrightarrow\;n=\frac{\ln(K_{n})-\ln(K_{0})}{\ln(1+p)}=\frac{\ln(502,49)-\ln(400)}{\ln(1,079)}\approx3\\[-11pt]&\end{align*}\) \(\begin{align*}\displaystyle(3)\;K_{n}=K_{0}\cdot(1+p)^n\;&\Longleftrightarrow\;\sqrt[n]{\frac{K_{n}}{K_{0}}}=1+p\\&\Longleftrightarrow\;p=\sqrt[n]{\frac{K_{n}}{K_{0}}}-1=\sqrt[4]{\frac{4862,03\,€}{4000\,€}}-1\approx0,05=5\,\%\\[-11pt]&\end{align*}\) \(\begin{align*}\displaystyle(4)\;K_{n}=K_{0}\cdot(1+p)^n\;&\Longleftrightarrow\;K_{0}=\frac{K_{n}}{(1+p)^n}=\frac{8933,59\,€}{\left(1+\frac{1}{100}\right)^5}\approx8500\,€\end{align*}\)

Aufgabe 2

Das Kapital das wir im ersten Jahr einzahlen wird zunächst ein Jahr lang mit 1 % verzinst. Damit sind am Ende des Jahres

\(\displaystyle K_{1}=1000\,€\cdot\left(1+\frac{1}{100}\right)^{1}=1010\,€\)

angespart. Nun werden erneut 1000 € eingezahlt so dass im zweiten Jahr nun ein Kapital von insgesamt 2010 € mit 2 % verzinst wird. Wir erhalten

\(\displaystyle K_{2}=2010\,€\cdot\left(1+\frac{2}{100}\right)^1=2050,20\,€\,.\)

Stellen wir das Ergebnis in Abhängigkeit der jährlichen Zuzahlungen von \(K_{0}=1000\,€\) dar, erhalten wir

\(\displaystyle K_{2}=\big(K_{1}+K_{0}\big)\cdot\left(1+\frac{2}{100}\right)=\left(K_{0}\cdot1,01+K_{0}\right)\cdot1,02=\underbrace{K_{0}\cdot1,01\cdot1,02}_{T1}+\underbrace{K_{0}\cdot1,01}_{T2}\,.\)

Dabei entspricht der Term T1 dem Anteil am angesparten Kapital, der durch Verzinsung der ersten Einzahlung entsteht und T2 dem Anteil, der durch Verzinsung der zweiten Einzahlung entsteht. Aus dieser Struktur können wir sofort eine Formel für das Kapital nach fünf Jahren ableiten:

\(\begin{align*}K_{5}&=K_{0}\cdot1,01\cdot1,02\cdot1,03\cdot1,04\cdot1,05+K_{0}\cdot1,02\cdot1,03\cdot1,04\cdot1,05\\&\phantom{=}+K_{0}\cdot1,03\cdot1,04\cdot1,05+K_{0}\cdot1,04\cdot1,05+K_{0}\cdot1,05\\&=1000\,€\cdot\big(1,01\cdot1,02\cdot1,03\cdot1,04\cdot1,05+1,02\cdot1,03\cdot1,04\cdot1,05\\&\phantom{=}+1,03\cdot1,04\cdot1,05+1,04\cdot1,05+1,05\big)\approx5572,74\,€\end{align*}\)

Alternativ können wir auch schrittweise das Kapital am Ende jeden Jahres berechnen. Wir haben bereits

\(K_{1}=1010\,€\;\,\text{ sowie }\;\,K_{2}=2050,20\,€\)

und erhalten damit für das Kapital

• nach drei Jahren: \(\displaystyle K_{3}=3050,20\,€\cdot\left(1+\frac{3}{100}\right)^1=3141,706\,€\\[11pt]\)
• nach vier Jahren: \(\displaystyle K_{4}=4141,706\,€\cdot\left(1+\frac{4}{100}\right)^1=4307,37424\,€\\[11pt]\)
• nach fünf Jahren: \(\displaystyle K_{5}=5307,37424\,€\cdot\left(1+\frac{5}{100}\right)^1\approx5572,74\,€\\[11pt]\)