Kapitel 13: Tipps und Tricks zum Lösen von Aufgaben (S. 221)
Aufgabe 1
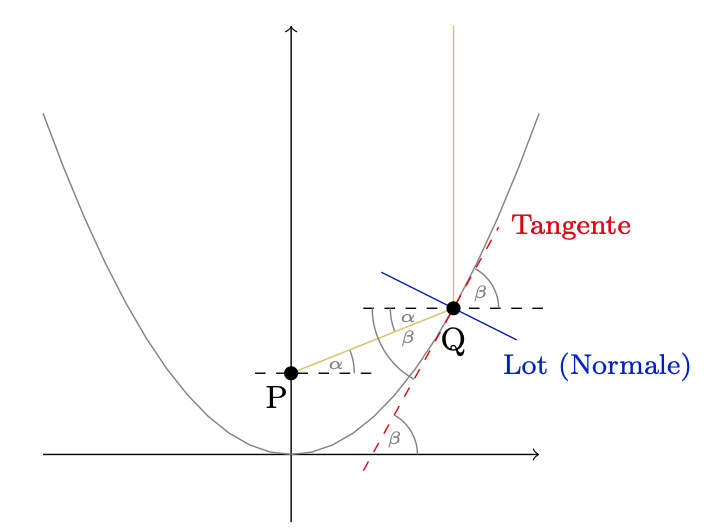
Eine Skizze ist hier sehr hilfreich. Dazu betrachten wir einen beliebigen Strahl, der in einem beliebigen Punkt \(Q(x|a\cdot x^2)\) auf die Parabel trifft und dann in den Punkt P (in dem sich alle Strahlen treffen) reflektiert wird. Aufgrund der Achsensymmetrie der Parabel muss dieser Punkt auf der Mittelachse liegen, also gemäß unserer Skizze von der Form \(P(0|y)\) sein.
Die zentrale Idee hier ist das sogenannte „Reflexionsgesetz“, das besagt, dass der einfallende und der reflektierte Strahl den gleichen Winkel zum Lot einschließet. Übertragen auf den Strahl der auf die Parbel fällt können wir der Skizze entnehmen, dass
\(\begin{alignat*}{2}&&90^{\circ}-\big(\beta-\alpha\big)&=90^{\circ}-\big(90^{\circ}-\beta)\\&\Longleftrightarrow\quad&90^{\circ}+\alpha&=2\cdot\beta-\alpha\,.\end{alignat*}\)
Der Winkel \(\alpha\) entspricht gerade dem Steigungswinkel der Geraden durch P und Q, d.h.
\(\tan(\alpha)=m_{P,Q}=\frac{a\cdot x^2-y}{x-0}=\frac{a\cdot x^2-y}{x},\)
und der Winkel \(\beta\) entspricht dem Steigungswinkel der Tangente, also
\(\tan(\beta)=f'(x)=2a\cdot x\,.\)
Aus dem Reflexionsgesetz folgt jetzt, dass
\(\tan(\beta-\alpha)=\tan(90^{\circ}-\beta)=\frac{\sin(90^{\circ}-\beta)}{\cos(90^{\circ}-\beta)}=\frac{\cos(\beta)}{\sin(\beta)}=\frac{1}{\tan(\beta)}\,.\)
Mit dem Additionstheorem für den Tangens
\(\begin{align*}\tan(r+s)=\frac{\tan(r)-\tan(s)}{1+\tan(r)\tan(s)}\end{align*}\)
folgt (da \(0<\alpha,\beta<90^{\circ}\))
\(\begin{alignat*}{2}&&\tan(\beta-\alpha)&=\frac{1}{\tan(\beta)}\\&\Longleftrightarrow\qquad&\frac{\tan(\beta)-\tan(\alpha)}{1+\tan(\beta)\tan(\alpha)}&=\frac{1}{\tan(\beta)}\\&\Longleftrightarrow\qquad&\tan^2(\beta)-\tan(\alpha)\tan(\beta)&=1+\tan(\beta)\tan(\alpha)\\&\Longleftrightarrow\qquad&\tan^2(\beta)-2\tan(\alpha)\tan(\beta)=1\\&\Longleftrightarrow\qquad&\big(2a\cdot x\big)^2-2\cdot\big(2a\cdot x\big)\cdot\left(\frac{ax^2-y}{x}\right)&=1\\&\Longleftrightarrow\qquad&4a^2\cdot x^2-4a\cdot(a\cdot x^2-y)&=1\\&\Longleftrightarrow\qquad&4a^2x^2-4a^2x^2+4ay&=1\\&\Longleftrightarrow\qquad&y&=\frac{1}{4a}\,.\end{alignat*}\)
Der Punkt P an dem der Strahl die y-Achse trifft ist also tatsächlich unabhängig von x (und damit vom Punkt Q in dem der Strahl die Parabel trifft). Es treffen sich also alle Strahlen in diesem Punkt.
Aufgabe 2
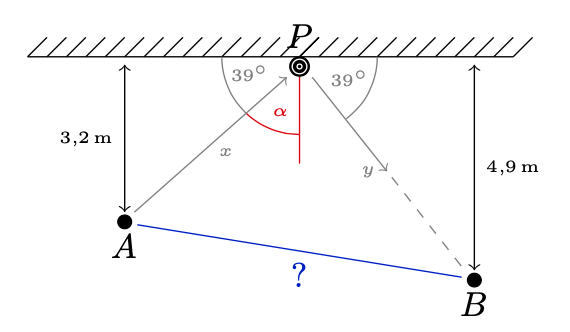
Auch für die „Reflexion“ des Pucks an der Bande gilt das Reflexionsgesetz, d.h. ein- und ausfallender Winkel sind gleich. Das bedeutet, dass der Winkel bei P tatsächlich \(2\alpha\) ist. Nun ist zunächst einmal
\(90^{\circ}=39^{\circ}+\alpha\;\Longleftrightarrow\;\alpha=51^{\circ}\,,\)
und andererseits können wir mit dem Sinus die beiden Längen \(x\) und \(y\) berechnen.
Es gilt nämlich:
\(\begin{alignat*}{2}&&\sin(39^{\circ})=\frac{3,2\,m}{x}\qquad&\text{und}\qquad\sin(39^{\circ})=\frac{4,9\,m}{y}\\&\Longleftrightarrow\qquad&x=\frac{3,2}{\sin(39^{\circ})}\,m\qquad&\text{und}\qquad y=\frac{4,9}{\sin(39^{\circ})}\,m\,.\end{alignat*}\)
Aus dem Kosinusse folgt nun für die gesuchte Seitenlänge c:
\(\begin{align*}c^2&=x^2+y^2-2\cdot x\cdot y\cdot\cos(2\alpha)\\&=\left(\frac{3,2}{\sin(39^{\circ})}\,m\right)^2+\left(\frac{4,9}{\sin(39^{\circ})}\,m\right)^2-2\cdot\frac{3,2}{\sin(39^{\circ})}\,m\cdot\frac{4,9}{\sin(39^{\circ})}\,m\cdot\cos(102^{\circ})\\&=\frac{3,2^2\,m^2+4,9^2\,m^2-31,36\,m^2\cdot\cos(102^{\circ})}{\sin^2(39^{\circ})}\approx102,9433\,m^{2}\,,\end{align*}\)
also \(c\approx\sqrt{102,9433\,m^2}\approx10,15\,m\,.\)
Aufgabe 3
Für den Kolbenweg \(x\) müssen wir die Länge \(c\) der Grundseite des abgebildeten Dreiecks von der Gesamtlänge \(r+l\) abziehen, d.h. \(x=r+l-c\,.\)
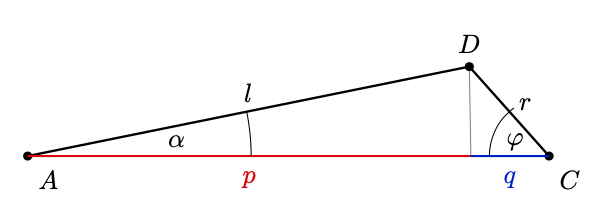
Für die Grundseite \(c\) betrachten wir das Dreieck etwas genauer. Es ist \(c=p+q\) und aus der Skizze folgt sofort
\(p=\cos(\alpha)\cdot l\qquad\text{und}\qquad q=\cos(\varphi)\cdot r\)
und damit
\(x=r+l-\cos(\alpha)\cdot l-\cos(\varphi)\cdot r=\big(1-\cos(\alpha)\big)\cdot l+\big(1-\cos(\varphi)\big)\cdot r\,.\)Der Kolbenweg hängt also noch von den beiden Variablen \(\alpha\) und \(\varphi\) ab, von denen wir jetzt noch eine eliminieren wollen. Mit dem Sinussatz erhalten wir
\(\frac{l}{\sin(\varphi)}=\frac{r}{\sin(\alpha)}\;\Longleftrightarrow\;\sin(\alpha)=\frac{r}{l}\cdot\sin(\varphi)\)
und außerdem liefert der „trigonometrische Pythagoras“ (da \(-90^{\circ}<\alpha<90^{\circ}\)
\(\cos^2(\alpha)+\sin^2(\alpha)=1\;\Longleftrightarrow\;\cos(\alpha)=\sqrt{1-\sin^2(\alpha)}=\sqrt{1-\left(\frac{r}{l}\right)^2\cdot\sin^2(\varphi)}\,.\)
Wir erhalten schließlich
\(\boxed{\,x=\left(1-\sqrt{1-\left(\frac{r}{l}\right)^2\cdot\sin^2(\varphi)}\right)\cdot l+\big(1-\cos(\varphi)\big)\cdot r\,}\,.\)
Da wir den zeitlichen Verlauf des Kolbenweges bestimmen sollen, müssen wir nun die Variable \(\varphi\) durch die Zeit \( t \) ersetzen. Wegen der gleichmäßigen Drehung der Kurbelwelle ist aber \(\varphi=\omega\cdot t\) und somit
\(\boxed{\,x=x(t)=\left(1-\sqrt{1-\left(\frac{r}{l}\right)^2\cdot\sin^2(\omega\cdot t)}\right)\cdot l+\big(1-\cos(\omega\cdot t)\big)\cdot r\,}\,.\)
(a) Offensichtlich ist die oben bestimmte Formel für den Kolbenweg recht kompliziert. Daher vereinfachen wir sie nun indem wir den Wurzelterm näherungsweise durch die Tangente der zugehörigen Funktion ersetzen. Dazu bestimmen wir zunächst einmal die Tangente an \(f(z)=\sqrt{1-z}\) bei \(z=0\).
Es ist \(f'(z)=-\frac{1}{2\cdot\sqrt{1-z}}\) und mit der Formel von Seite 142 folgt:
\(\begin{align*}t(z)&=f'(0)\cdot(z-0)+f(0)\\&=-\frac{1}{2\cdot\sqrt{1-0}}\cdot(z-0)+\sqrt{1-0}=-\frac{1}{2}z+1\,.\end{align*}\)
Damit vereinfacht sich die ursprüngliche Funktion zu
\(\begin{align*}x(t)&=\left(1-\sqrt{1-\left(\frac{r}{l}\right)^2\cdot\sin^2(\omega\cdot t)}\right)\cdot l+\big(1-\cos(\omega\cdot t)\big)\cdot r\,\\&\approx\left(1-\left(-\frac{1}{2}\cdot\left(\frac{r}{l}\right)^2\cdot\sin^2(\omega\cdot t)+1\right)\right)\cdot l+\big(1-\cos(\omega\cdot t)\big)\cdot r\\&=\frac{r^2}{2\cdot l}\cdot\sin^2(\omega\cdot t)+\big(1-\cos(\omega\cdot t)\big)\cdot r\,.\end{align*}\)
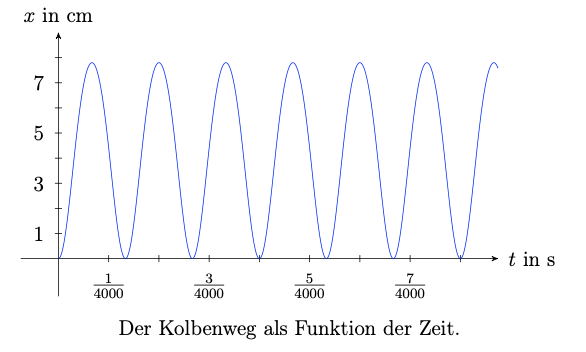
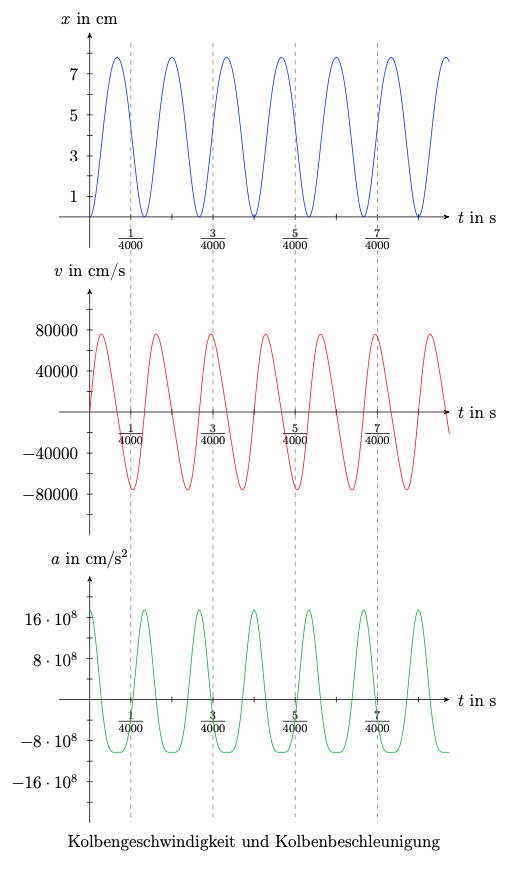
Mit den gegebenen Werten für \(r,\;l\) und \(\omega\) erhalten wir damit den Graphen
(b) Für den zeitlichen Verlauf der Kolbengeschwindigkeit und -beschleunigung, müssen wir die erste und zweite Ableitung des Kolbenweges bestimmen. Dabei gehen wir von der Näherung aus und erhalten:
\(\begin{align*}v(t)=x'(t)&=\frac{r^2}{2\cdot l}\cdot2\cdot \sin(\omega\cdot t)\cdot\cos(\omega\cdot t)\cdot \omega+\sin(\omega\cdot t)\cdot\omega\cdot r\\&=\omega r\cdot\sin(\omega\cdot t)\cdot\left(\frac{r}{l} \cdot\cos(\omega\cdot t)+1\right)\\[11pt]a(t)=v'(t)&=\omega r\cdot\cos(\omega\cdot t)\cdot\omega\cdot\left(\frac{r}{l} \cdot\cos(\omega\cdot t)+1\right)+\omega r\cdot\sin(\omega\cdot t)\cdot\left(-\frac{\omega r}{l}\cdot\sin(\omega\cdot t)\right)\\&=\frac{\omega^2\cdot r^2}{l}\cdot\left(\cos^2(\omega\cdot t)-\sin^2(\omega\cdot t)\right)+\omega^2 r\cdot\cos(\omega\cdot t)\,.\end{align*}\)
Aufgabe 4
In jedem der vier Knotenpunkte kann nur soviel Strom abfließen wie auch hineinfliegt. Entsprechend erhalten wir die vier Gleichungen:
\(\begin{align*}\begin{array}{ccccccccc}I_1 & + & I_2 & & & & & = & I_A\\& – & I_2 & + & I_3 & & & = & I_B\\& & & & I_3 & – & I_4 & = & I_C\\I_4 & & & & & + & I_4 & = & I_D\end{array}\end{align*}\)
Da $I_D$ allerdings nicht bekannt ist, ersetzen wir die letzte Gleichung durch die Spannungsbilanz:
\(U_1+U_2+U_3+U_4+U_q=0\;\Longleftrightarrow\;R_1\cdot I_1-R_2\cdot I_2-R_3\cdot I_3-R_4\cdot I_4=-U_q\)
Wir erhalten das lineare Gleichungssystem
\(\begin{align*}\begin{pmatrix}1 & 1 & 0 & 0\\0 & -1 & 1 & 0\\0 & 0 & 1 & -1&\\R_1 & -R_2 & -R_3 & -R_4\end{pmatrix}\cdot\left(\begin{array}{c} I_1\\I_2\\I_3\\I_4\end{array}\right)=\left(\begin{array}{c}I_A\\I_B\\I_C\\-U_q\end{array}\right).\end{align*}\)
Setzen wir die vorgegebenen Werte ein und verwenden den Gaußalgorithmus, erhalten wir:
\(\begin{align*}\left(\begin{array}{rrrr|r}1 & 1 & 0 & 0 & 2 \\0 & 1 & -1 & 0 & -1 \\0 & 0 & 1 & -1 & 1 \\1 & -2 & -5 & -2 & -19\end{array}\right)&\xrightarrow[]{-1\cdot\text{(I)}+\text{(IV)}}\left(\begin{array}{rrrr|r}1 & 1 & 0 & 0 & 2 \\0 & 1 & -1 & 0 & -1 \\0 & 0 & 1 & -1 & 1 \\0 & -3 & -5 & -2 & -21\end{array}\right)\\&\xrightarrow[]{\,3\cdot\text{(II)}+\text{(IV)}\,}\left(\begin{array}{rrrr|r}1 & 1 & 0 & 0 & 2 \\0 & 1 & -1 & 0 & -1 \\0 & 0 & 1 & -1 & 1 \\0 & 0 & -8 & -2 & -24\end{array}\right)\\&\xrightarrow[]{8\cdot\text{(III)}+\text{(IV)}}\left(\begin{array}{rrrr|r}1 & 1 & 0 & 0 & 2 \\0 & 1 & -1 & 0 & -1 \\0 & 0 & 1 & -1 & 1 \\0 & 0 & 0 & -10 & -16\end{array}\right)\\&\xrightarrow[]{\;\text{(IV)}:(-10)\;}\left(\begin{array}{rrrr|r}1 & 1 & 0 & 0 & 2 \\0 & 1 & -1 & 0 & -1 \\0 & 0 & 1 & -1 & 1 \\0 & 0 & 0 & 1 & 1,6 \\\end{array}\right)\\&\xrightarrow[\,\text{(IV)}+\text{(III)}\,]{\,-1\cdot\text{(II)}+\text{(I)}\,}\left(\begin{array}{rrrr|r}1 & 0 & 1 & 0 & 3 \\0 & 1 & -1 & 0 & -1 \\0 & 0 & 1 & 0 & 2,6 \\0 & 0 & 0 & 1 & 1,6 \\\end{array}\right)\xrightarrow[\text{(III)}+\text{(II)}]{-1\cdot\text{(III)}+\text{(I)}}\left(\begin{array}{rrrr|r}1 & 0 & 0 & 0 & 0,4 \\0 & 1 & 0 & 0 & 1,6 \\0 & 0 & 1 & 0 & 2,6 \\0 & 0 & 0 & 1 & 1,6 \\\end{array}\right).\end{align*}\)
und somit
\(I_1=0,4\,\text{A},\;\,\;I_2=1,6\,\text{A},\;\,\;I_3=2,6\,\text{A},\;\,\;I_4=1,6\,\text{A}\,.\)