Kapitel 11: Integralrechnung (S. 186)
Aufgabe 1
(a) Es ist
\(\begin{align*}\int_{0}^{1}\frac{1}{4}x^3-x^2\,dx&=\frac{1}{4}\int_{0}^{1}x^3\,dx-\int_{0}^{1}x^2\,dx\\ &=\frac{1}{4}\Big[\frac{x^4}{4}\Big]_{0}^{1}-\Big[\frac{x^3}{3}\Big]_{0}^{1}\\&=\Big[\frac{x^4}{16}-\frac{x^3}{3}\Big]_{0}^{1}=\frac{1^4}{16}-\frac{1^3}{3}=-\frac{13}{48}\,.\end{align*}\)
(b) Substituieren wir \(z=2x+3\), also \(z’=2\) bzw. \(dz=2\,dx\), folgt
\(\begin{align*}\int_{1}^{1}\sqrt{2x+3}\,dx&=\int\limits_{2\cdot(-1)+3}^{2\cdot1+3}\sqrt{z}\cdot\frac{1}{2}\,dz\\ &=\frac{1}{2}\int_{1}^{5}z^{\frac{1}{2}}\,dz\\ &=\frac{1}{2}\cdot\Big[\frac{2}{3}z^{\frac{3}{2}}\Big]_{1}^{5}=\frac{1}{2}\cdot\Big(\frac{2}{3}\cdot5^{\frac{3}{2}}-\frac{2}{3}\cdot1^{\frac{3}{2}}\Big)=\frac{5}{3}\cdot\sqrt{5}-\frac{1}{3}\,.\end{align*}\)
(c) Wir integrieren zweimal partiell und folgen dabei unserer Faustformel, d.h. wir suchen eine Stammfunktion zu \(\cos(x)\) und leiten das Polynom \(x^2\) ab. Wir bekommen:
\(\begin{align*}\int_{0}^{\pi}\underbrace{x^2}_{=\,g(x)}\cdot\underbrace{\cos(x)}_{=\,f'(x)}\,dx&=\Big[\underbrace{x^2}_{=\,g(x)}\cdot\underbrace{\sin(x)}_{=\,f(x)}\Big]_{0}^{\pi}-\int_{0}^{\pi}\underbrace{2x}_{=\,g'(x)}\cdot\underbrace{\sin(x)}{=\,f(x)}\,dx\\&=\underbrace{\Big(\pi^2\cdot\sin(\pi)-0^2\cdot\sin(0)\Big)}_{=\,0}-2\int_{0}^{\pi}\underbrace{x}_{=\,g(x)}\cdot\underbrace{\sin(x)}_{=\,f'(x)}\,dx\\ &=-2\cdot\Big(\Big[\underbrace{x}_{=\,g(x)}\cdot\underbrace{(-\cos(x))}_{=\,f(x)}\Big]_{0}^{\pi}-\int_{0}^{\pi}\underbrace{1}_{=\,g'(x)} \cdot\underbrace{(-\cos(x))}_{=\,f(x)}\,dx\Big)\\ &=-2\cdot\Big(\big(-\pi\cdot\cos(\pi)+0\cdot\cos(0)\big)+\int_0^{\pi}\cos(x)\,dx\Big)\\&=-2\cdot\Big(\pi+\Big[\sin(x)\Big]_0^{\pi}\Big)=-2\cdot\Big(\pi+\underbrace{\big(\sin(\pi)-\sin(0)\big)}_{=\,0}\Big)=-2\pi\,.\end{align*}\)
(d) Auch hier hat sich leider der Fehlerteufel eingeschlichen. Statt bei 1 sollte das Integral bei 2 starten. Substituieren wir dann zunächst und zwar \(z=3x^2-4\). Dann ist
\(z’=6x\;\Longleftrightarrow\;dx=\frac{1}{6x}\,dz\)
und wir erhalten erstmal
\(\begin{align*}\int_{2}^{3}\ln(3x^2-4)\cdot x\,dx&=\int\limits_{3\cdot2^2-4}^{3\cdot3^2-4}\ln(z)\cdot x\cdot\frac{1}{6x}\,dz\\&=\frac{1}{6}\int_{8}{31}\ln(z)\,dz\,.\end{align*}\)
Entweder wir ziehen nun eine Formelsammlung zu Rate oder wir erinnern uns, dass wir \(\ln(z)\) auch als Produkt \(1\cdot \ln(z)\) schreiben können und verwenden die partielle Integration (wobei wir auch hier wieder gegen unsere Faustformel verstoßen). Dann folgt nämlich:
\(\begin{align*}\int_{8}^{31}\ln(z)\,dz&=\int_{8}^{31}\underbrace{1}_{=\,f'(z)}\cdot\underbrace{\ln(z)}_{=\,g(z)}\,dz\\&=\Big[\underbrace{z}_{=f(z)}\cdot\underbrace{\ln(z)}_{=\,g(z)}\Big]_{8}^{31}-\int_{8}^{31}\underbrace{z}_{=f(z)}\cdot\underbrace{\frac{1}{z}}_{=\,g'(z)}\,dz\\&=\Big[z\cdot\ln(z)\Big]_{8}^{31}-\int_{8}^{31}1\,dz\\&=\Big[z\cdot\ln(z)\Big]_{8}^{31}-\Big[z\Big]_{8}^{31}\\&=\Big[z\cdot\ln(z)-z\Big]_{8}^{31}=31\cdot\ln(31)-8\cdot\ln(8)-23\end{align*}\)
und somit
\(\begin{align*}\int_{2}^{3}\ln(3x^2-4)\cdot x\,dx&=\frac{31\ln(31)-8\ln(8)-23}{6}\,.\end{align*}\)
Aufgabe 2
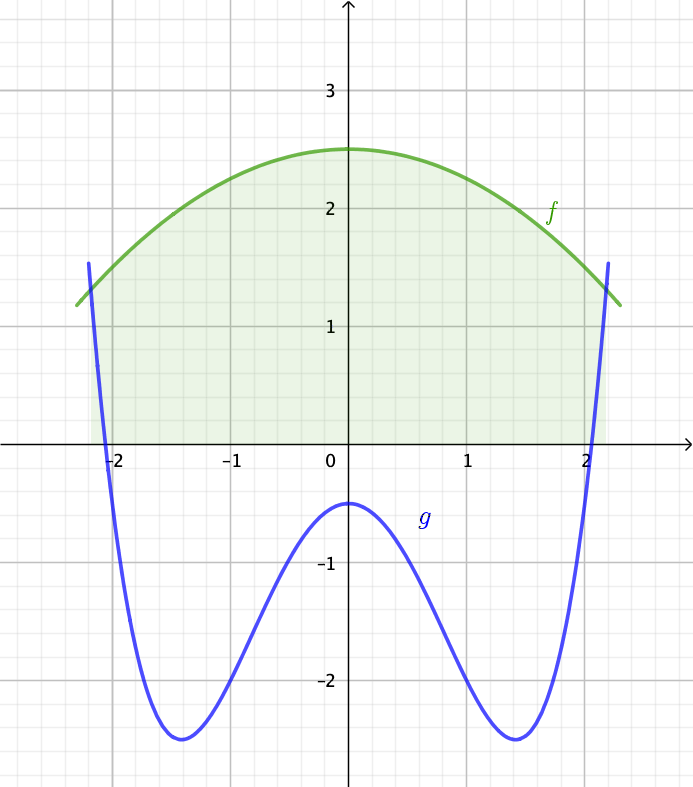
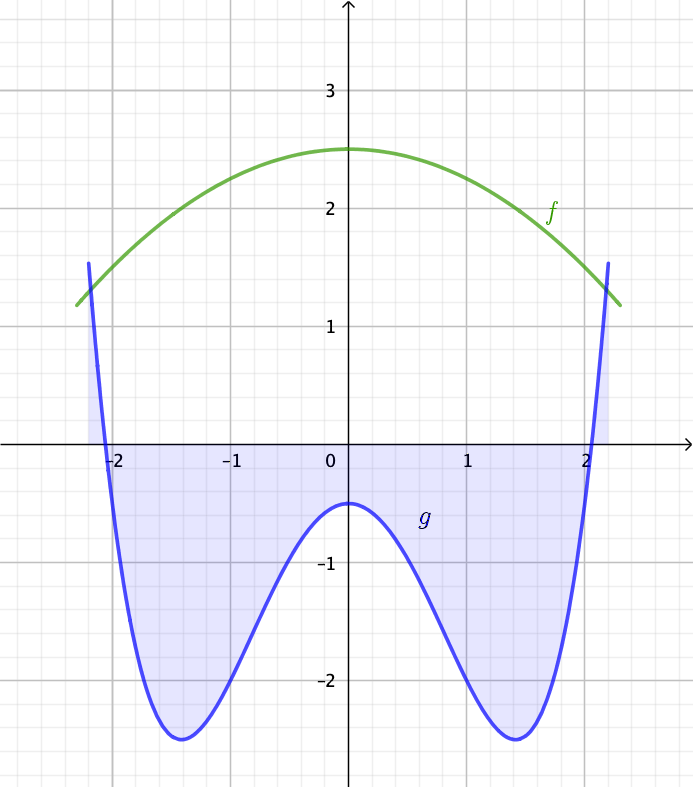
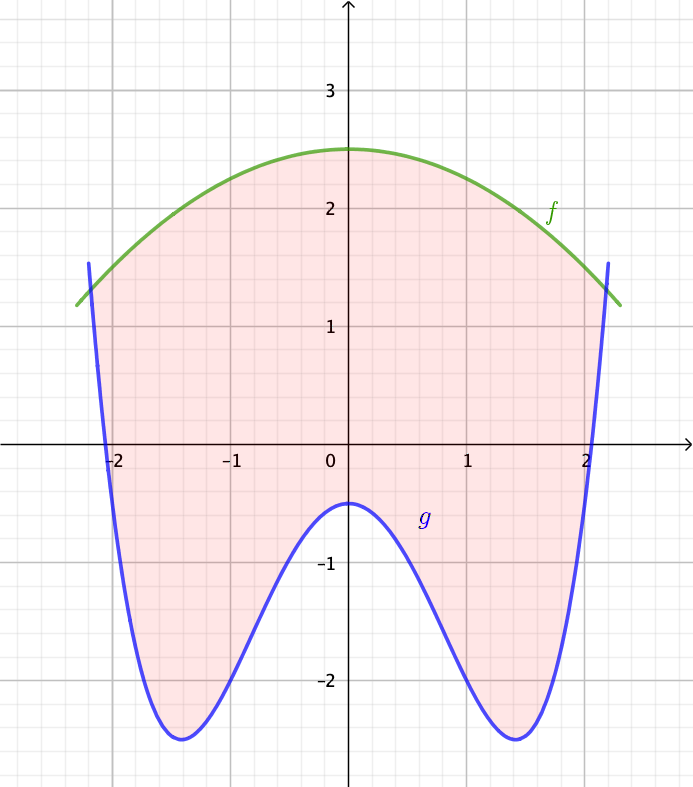
Wir müssen also in der Aufgabe die Fläche zwischen den beiden Funktionen berechnen. Ein Blick in die Skizzen zeigt, dass wir dazu einfach nur die Fläche die die Funktion \(g\) mit der x-Achse einschließt von der Fläche, die die Funktion \(f\) mit der x-Achse einschließt, abziehen müssen
(Beachte, dass Flächen unter der x-Achse vom Integral negativ berechnet werden. Ziehen wir diese also ab, addieren wir den Betrag der Fläche in Wahrheit.)
Übersetzt in die Sprache der Mathematik bedeutet das, dass wir
\(\begin{align*}A&=\int_{a}^{b} f(x)\,dx-\int_{a}^{b} g(x)\,dx\\&=\int_{a}^{b} f(x)-g(x)\,dx\\&=\int_{a}^{b}-\frac{1}{2}x^4+\frac{7}{4}x^2+3\,dx\\&=\Big[-\frac{1}{20}x^5+\frac{7}{12}x^3+3x\Big]_{a}^{b}\end{align*}\)
berechnen müssen. Dafür fehlen uns noch die Grenzen, die aber gerade den Stellen entsprechen, an denen sich \(f\) und \(g\) schneiden. Wir lösen also zunächst mal die Gleichung \(f(x)=g(x)\):
\(\begin{alignat*}{3}&&f(x)&=g(x)\qquad&&\\ &\Longleftrightarrow\quad& -\frac{1}{4}x^2+2,5&=\frac{1}{2}x^4-2x^2-\frac{1}{2}\qquad&&\Big|\;+\frac{1}{4}x^2-2,5\\&\Longleftrightarrow\quad & 0 &=\frac{1}{2}x^4-\frac{7}{4}x^2-3\qquad&&\Big|\;\cdot 2\\&\Longleftrightarrow\quad & 0 &=x^4-\frac{7}{2}x^2-6\qquad&&\end{alignat*}\)
Das ist nun offensichtlich eine Gleichung vierten Grades, die wir auf den ersten Blick garnicht so einfach lösen können. Aber wir lassen uns doch nicht gleich unterkriegen, sondern tricksen einfach ein wenig. Wir setzen einfach mal \(z=x^2\). Dann wird die Gleichung nämlich schnell zu einer quadratischen Gleichung:
\(\begin{alignat*}{3}&&f(x)&=g(x)\qquad&&\\ &\Longleftrightarrow\quad& x^4-\frac{7}{2}x^2-6&=0\qquad&&\Big|\;z=x^2\\ &\Longrightarrow\quad&z^2-\frac{7}{2}z-6&=0\qquad&&\Big|\;\,\text{p-q-Formel}\\&\Longleftrightarrow\quad& z_{1,2}&=\frac{7}{4}\pm\sqrt{\left(-\frac{7}{4}\right)^2+6}\qquad&&\\&\Longleftrightarrow\quad& z_{1,2}&=\frac{7}{4}\pm\sqrt{\frac{145}{16}}\qquad&&\\&\Longleftrightarrow\quad& z_{1,2}&=\frac{9\pm\sqrt{145}}{4}\qquad&&\end{alignat*}\)
Berücksichtigen wir nun, dass \(z=x^2\), also zum einen \(z\) positiv sein muss und somit
\(\displaystyle z=\frac{9+\sqrt{177}}{4}\)
die einzige z-Lösung dieser Gleichungen ist und zum anderen
\(z=x^2\;\Longleftrightarrow\;x=\pm\sqrt{z}\)
ist, erhalten wir für die x-Lösungen der ursprünglichen Gleichung
\(\displaystyle x_{1}=-\frac{1}{2}\sqrt{7+\sqrt{145}}\approx-2,18\;\text{ und }x_{2}=\frac{1}{2}\sqrt{7+\sqrt{145}}\approx2,18\,.\)
Rechnen wir mit den Näherungswerten weiter, erhalten wir eine Fläche von
\(\begin{align*}A&=\int_{-2,18}^{2,18} f(x)\,dx-\int_{a}^{b} g(x)\,dx=\Big[-\frac{1}{20}x^5+\frac{7}{12}x^3+3x\Big]_{-2,18}^{2,18}\approx15,32\,[\text{dm}^2]\,.\end{align*}\)
Das Logo hat also ein Volumen von
\(V\approx15,32\,\text{dm}^2\cdot0,2\,\text{dm}=3,064\,\text{dm}^3\,.\)
Aufgabe 3
Hier fehlt leider die Gesamtgröße der Datei, die sich gerade auf \(20\,\text{GB}=20.000\,\text{MB}\) beläuft.
(a) Nach \(0,5\,\text{min}\) wir die Datei mit durchschnittlich etwa \((1,11+1,3)/2\,\text{MB/s}=1,205\text{MB/s}=72,3\,\text{MB/min}\) heruntergeladen. Dementsprechend sollten in den ersten \(30\,\text{s}\) bereits ca. \(36,15\,\text{MB}\) übertragen worden sein und noch etwa \( 20.000-36,15=19963,85\,\text{MB}\) übertragen werden. Dafür bräuchte es dann noch
\(t=19963,85\,\text{MB}/72,3\,\text{MB/min}\approx276\,\text{min}=4\,\text{h}\,36\,\text{min}\,.\)
Entsprechend wird die Datei nach \(2\,\text{min}\) mit durchschnittlich
\((1,11+1,3+0,85+1,02)/2\,\text{MB/s}=2,14\,\text{MB/s}=128,4\,\text{MB/min}\)
heruntergeladen und es sind noch ca. \(20.000-256,8=19743,2\,\text{MB}\) zu übertragen. Dafür bräuchte es noch
\(t=19743,2\,\text{MB}/128,4\,\text{MB/min}\approx154\,\text{min}=2\,\text{h}\,34\,\text{min}\,.\)
(b) Wir suchen also eine Funktion vierten Grades, die den Verlauf der Übertragungsrate näherungsweise beschreibt. So eine Funktion hat die Form
\(u(x)=a\cdot x^4+b\cdot x^3+c\cdot x^2+d\cdot x+e\)
und wir müssen die Koeffizienten \(a,\;b,\;c,\;d,\;e\) festlegen. Dazu nutzen wir die gegebenen Funktionswerte. Runden wir auf die erste Nachkommastelle (zur Vereinfachung – es soll ja nur Näherungsweise beschrieben werden), multiplizieren mit 60 (um die Übertragunsrate in MB/min. umzurechnen) erhalten wir gerade
\(u(0)=66\,,\quad u(0,5)=78\,,\quad u(1,2)=54\,,\quad u(2)=60\,,\quad u(2,4)=54\)
Das liefert ein zugegebenermaßen sehr großes Gleichungssystem:
\(\begin{align*} a\cdot 0^4+b\cdot0^3+c\cdot0^2+d\cdot 0+e&=66\\ a\cdot 0,5^4+b\cdot0,5^3+c\cdot0,5^2+d\cdot0,5+e&=78\\ a\cdot 1,2^4+b\cdot1,2^3+c\cdot1,2^2+d\cdot1,2+e&=54\\ a\cdot 2^4+b\cdot2^3+c\cdot2^2+d\cdot2+e&=60\\ a\cdot 2,4^4+b\cdot2,4^3+c\cdot2,4^2+d\cdot2,4+e&=54\end{align*}\)
Mit einiger Rechnerei (oder einem entsprechenden Taschenrechner) folgt damit, dass
\(u(x)\approx-26,14x^4+134,9x^3-218,1x^2+320,7x+66\,.\)
(Hinweis: In dieser Aufgabe geht es nur darum EINE Funktion vierten Grades zu finden, die die Messwerte beschreibt. Es muss nicht die bestmögliche sein. Deine Funktion und auch deine Herangehensweise kann also auch anders aussehen.)
(c) Vergleichen wir die Werte der Tabelle mit den Werten die wir mit der Funktion \(u\) berechnen können
\(\begin{alignat*}{6} &\text{Vergangene Zeit} &\;\;&0\;\;&\;\;&0,5\;\;&\;\;&1,2\;\;&\;\;&2\;\;&\;\;&2,4\;\;\\\hline &\text{Übertragungsrate in MB/min} \quad&\;\;&66\;\;&\;\;&187,5\;\;&\;\;&315,7\;\;&\;\;&496\;\;&\;\;&577\;\;\\\hline &\text{Übertragungsrate in MB/s} &\;\;&1,1\;\;&\;\;&3,1\;\;&\;\;&6,3\;\;&\;\;&8,3\;\;&\;\;&9,6\;\;\end{alignat*}\)
Während also in den gegebenen Daten die Übertragungsrate nach 1,2 min. und auch nach 2,4 min. zurückgegangen ist, steigt die von uns bestimmte Funktion durchgehend an. Die wirkliche Übertragungsrate wäre also wahrscheinlich zwischen 0,5 und 1,2 Minuten gefallen und ebenfalls zwischen 2 und 2,4 Minuten.
(d) Da unsere Funktion nur die Übertragungsgeschwindigkeit beschreibt, also die Änderungsrate der Datenmenge, müssen wir die Funktion integrieren. Wir suchen also \(T\) so dass
\(\int_0^Tu(x)\,dx=400\,.\)
Berechnen wir das Integral, erhalten wir
\(\begin{align*}\int_0^Tu(x)\,dx&=\int_{0}^T-26,14x^4+134,9x^3-218,1x^2+320,7x+66\,dx\\ &=\Big[-\frac{2614}{500}x^5+\frac{1349}{40}x^4-\frac{2181}{30}x^3+\frac{320,7}{2}x^2+66x\Big]_{0}^T\\&=-5,228T^5+33,725T^4-72,7T^3+160,35T^2+66T\end{align*}\)
und müssen also T so bestimmen, dass
\(-5,228T^5+33,725T^4-72,7T^3+160,35T^2+66T=400\,\)
ist. Mit einem Computer oder Taschenrechner erhalten wir \(T=1,64\,\)min.
Aufgabe 4
(a) Die Abbildung beschreibt also die Geschwindigkeit mit der der Ballon steigt (Geschwindigkeit positiv) bzw. fällt (Geschwindigkeit negativ). Entsprechend steigt der Ballon in den ersten ca. \(46\,\text{min.}\), wobei er nach \(40\,\text{min.}\) am schnellsten steigt. Nach diesen \(46\,\text{min.}\) sinkt er dann wobei er seine höchste Sinkgeschwindigkeit bei \(60\,\text{min.}\) erreicht.
(b) Da die Geschwindigkeit in vertikaler Richtung gerade der Änderungsrate der Höhe entspricht, ist die exakte Höhe durch die Fläche unter der Funktion gegeben.
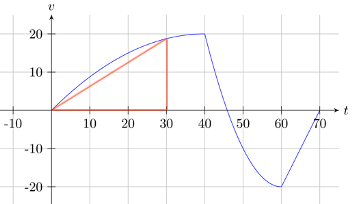
Da die Funktionsgleichung nicht bekannt ist können wir das Integral zur Bestimmung dieser Fläche aber nicht nutzen. Näherungsweise entspricht die Fläche aber gerade dem abgebildeten Dreieck.
Dessen Flächeninhalt ist gerade
\(\displaystyle A_{\Delta}=\frac{1}{2}\cdot30\cdot18=270\)
so dass der Ballon wohl nach \(30\,\text{min.}\) etwa eine Höhe von \(270\,\text{m}\) erreicht. Seine maximale Höhe erreicht er nach ca. \(46\,\text{min.}\) und erreicht dabei schätzungsweise eine Höhe von
\(\displaystyle H=\frac{1}{2}\cdot40\,\text{min.}\cdot20\,\text{m/min.}+\frac{1}{2}\cdot6\,\text{min.}\cdot20\,\text{m/min.}=460\,\text{m}\,.\)
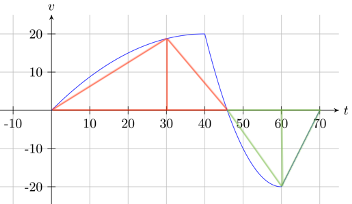
(das entspricht der Fläche der roten Dreiecke). Bis zum Ende der Ballonfahrt sinkt er dann um ca.
\(\begin{align*}H&=\frac{1}{2}\cdot14\,\text{min.}\cdot20\,\text{m/min.}\\&\quad+\frac{1}{2}\cdot10\,\text{min.}\cdot20\,\text{m/min.}=240\,\text{m}\,.\end{align*}\)
(das entspricht der Fläche der blauen Dreiecke). Die Fahrt endet also in einer Höhe von \(\displaystyle 460\,\text{m}-240\,\text{m}=220\,\text{m}\,.\)
Aufgabe 5
Wir müssen also das Rotationsvolumen bestimmen, das entsteht, wenn die Funktion \(f\) um die x-Achse rotiert und davon das Volumen des Lochs in der Mitte abziehen. ‚Dazu bestimmen wir zunächst mal die Funktion \(f\).
Wir wissen aus der Skizze, dass \(f(50)=550\) und \(f(40)=600\) sein muss. Entsprechend erhalten wir das Gleichungssystem
\(\begin{align*}a\cdot6.250.000+b&=550\\a\cdot2.560.000+b&=600\end{align*}\)
dessen Lösung gerade
\(\displaystyle a=-\frac{5}{369}\cdot 10^{-3}\quad\text{und}\quad b=\frac{2342}{369}\cdot 10^2\,.\)
Für das Rotationsvolumen folgt damit
\(\begin{align*}V_{R}&=\pi\int_{-50}^{50}\big(f(x)\big)^2\,dx\\&=\pi\cdot\int_{-50}^{50}\big(a\cdot x^4+b\big)^2\,dx\\&=\pi\cdot\int_{-50}^{50}a^2x^8+2abx^4+ab\,dx\\&=\pi\cdot\Big[\frac{a^2}{9}x^9+\frac{2ab}{5}x^5+ab\cdot x\Big]_{-50}^{50}\\&=2\cdot\pi\cdot\Big(\frac{a^2}{9}\cdot50^9+\frac{2ab}{5}\cdot 50^5+ab\cdot 50\Big)\approx3,8\cdot10^7\cdot\pi\;[\text{mm}^3]\,.\end{align*}\)
Das Loch in der Mitte hat einen Radius von \(50\,\text{mm}\) und eine Tiefe von \(100\,\text{mm}\), also ein Volumen von
\(V_{L}=\pi\cdot50^2\cdot 100=2,5\cdot10^5\cdot\pi\,[\text{mm}^3]\,.\)
Entsprechend hat die Riemenscheibe ein Volumen von \(V=V_{R}-V_{L}\approx1,2\cdot10^8\,\text{mm}^3\) und wiegt ca.
\(\displaystyle M=1,2\cdot10^5\,\text{cm}^3\cdot7,2\frac{\text{g}}{\text{cm}^3}=864\,\text{kg}\,.\)