Kapitel 10: Differenzialrechnung (S. 153)
Aufgabe 1
(a) Es gilt \(f'(x)=e^{2x^2+2x-3}\cdot (4x+2)\).
Die einzige Nullstelle der Ableitung ergibt sich somit für \(x=-\frac{1}{2}\), was somit einen Kandidaten für eine lokale Extremstelle erfüllt, da das notwendige Kriterium erfüllt ist.
Es gilt außerdem \(f“(x)=e^{2x^2+2x-3}\cdot (4x+2)^2+e^{2x^2+2x-3}\cdot 4\)
Daraus folgt \(f“(-\frac{1}{2})=e^{2(-\frac{1}{2})^2+2(-\frac{1}{2})-3}\cdot 4>0\), da die natürliche Exponentialfunktion niemals negativ oder null wird. Entsprechend handelt es sich bei \(x_t=-\frac{1}{2}\) um einen lokalen Tiefpunkt. Seine Koordinaten liegen bei \((-\frac{1}{2}|f(-\frac{1}{2}))\approx(-\frac{1}{2}|0,0301978)\).
(b) Es gilt \(g'(x)=3x^2+2x-2\).
Z.B. mithilfe der pq-Formel erhält man die beiden Nullstellen \(x_1=\frac{-\sqrt{7}-1}{3}\approx-1,22\) sowie \(x_2=\frac{\sqrt{7}-1}{3}\approx 0,55\).
Die zweite Ableitung lautet \(g“(x)=6x+2\), womit \(g“(-1,22)=-5,32<0\) sowie \(g“(0,55)=5,3>0\) folgt. Somit handelt es sich bei \(x_1\approx -1,22\) um einen Hochpunkt, bei \(x_2\approx 0,55\) um einen Tiefpunkt. Die Koordinaten lauten \((-1,22|2,11)\) bzw. \((0,55|-0,63)\).
(c) Es gilt \(h'(x)=4x^3+9x^2=x^2\cdot (4x+9)\).
Diese ist für \(x=0\) oder \(4x+9=0\) null. Aus Letzterem folgt \(x=-\frac{9}{4}\).
Probieren wir hier doch einmal das Vorzeichenwechselkriterium aus (Tipp über der Aufgabenstellung): Was passiert mit dem Vorzeichen von \(h‘\), wenn die Funktionswerte \(x=-\frac{9}{4}=-2,25\) überschreiten?
Es gilt \(h'(-2,3)=-1,058\) und \(h'(-2,2)=0,968\). Die Ableitungsfunktion wechselt beim Überschreiten von \(x\) also offenbar das Vorzeichen vom Negativen ins Positive. Dies kann nur bei einem lokalen Tiefpunkt der Fall sein (Bei einem Hochpunkt wäre es genau andersherum). Seine Koordinaten liegen bei \((-2,25|-6,54297)\).
Betrachten wir den zweiten Kandidaten \(x=0\): Es gilt z.B. \(h'(-0,1)=0,086\) und \(h'(0,1)=0,094\). Es findet also kein Vorzeichenwechsel statt. Folglich kann es sich weder um einen Tief- noch einen Hochpunkt handeln. Es muss daher einen Sattelpunkt geben. Seine Koordinaten lauten \((0|2)\).
Natürlich hätte man das auch alles mithilfe der zweiten Ableitung wie in (a) oder (b) lösen können. Wir wollten dir aber beides mal zeigen.
Aufgabe 2
Im Folgenden siehst du den Graphen der genannten Funktion.
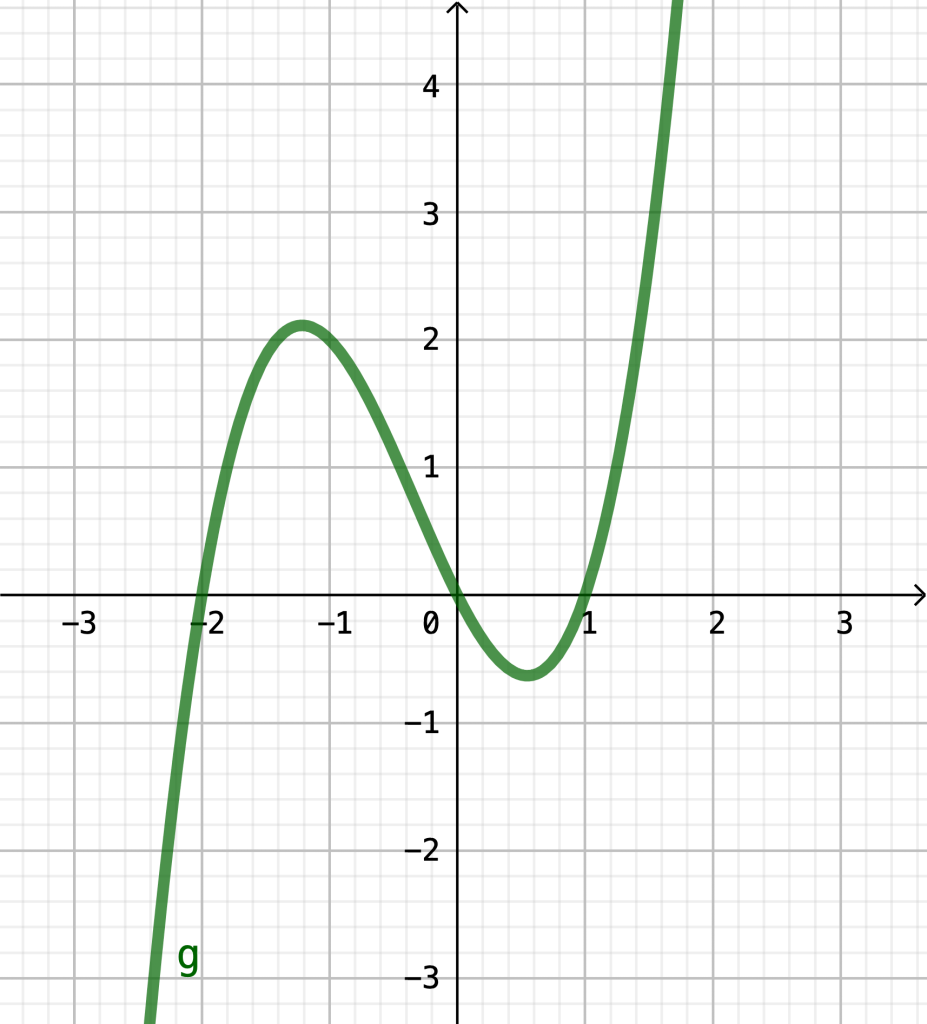
(a) Wenn wir die Funktion nur auf dem genannten Intervall betrachten ist der global tiefste Punkt bei \(x\approx 0,55\) – dem zuvor berechneten lokalen Tiefpunkt. Der global höchste Punkt ist bei \(x=2\).
(b) Der global tiefste Punkt ist wieder bei \(x\approx 0,55\), der global höchste bei \(x=-1\).
(c) Der global tiefste Punkt ist bei \(x=-3\), der global höchste bei \(x=2\)
(d) In diesem Fall gibt es keinen global tiefsten oder höchsten, da die Funktion unendlich kleine bzw. unendlich große Werte besitzt, bewegt man sich auf der x-Achse beliebig nach links bzw. rechts.