Kapitel 10: Differenzialrechnung (S. 145)
Aufgabe 1
(a) \(f'(x)=9x^2+4x-3\)
(b) \(g'(x)=0\)
(c) \(h'(x)=n\cdot x^{n-1}\), außer für \(n=1\). In diesem Fall gilt \(h'(x)=1\).
Aufgabe 2
Z.B. funktioniert dies für die Funktion \(f(x)=-\frac{2}{3}x^3+\frac{1}{2}x^2-x\). Beliebig viele weitere Funktionen erhältst du, indem du am ende eine beliebige konstante Zahl aufaddierst oder abziehst, denn diese fällt ja beim Ableiten weg.
Aufgabe 3
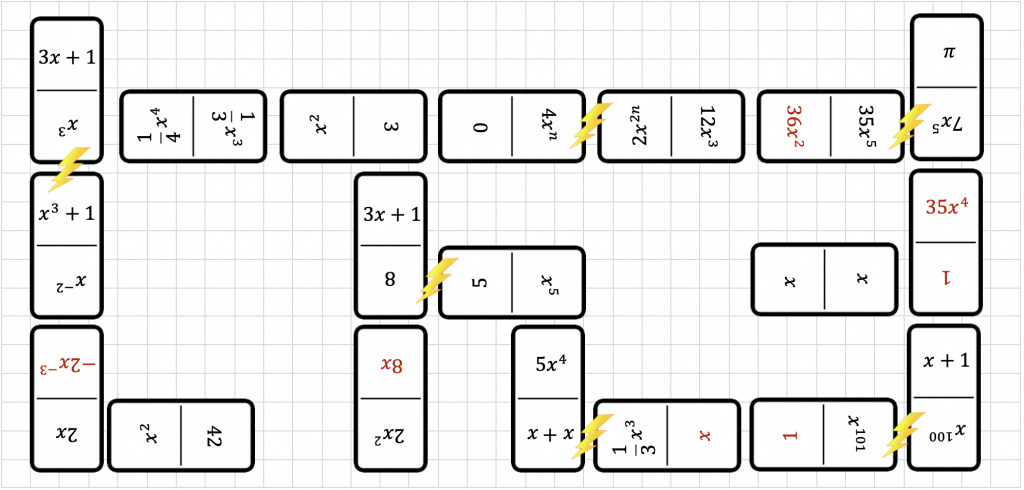
Fehler haben wir mit einem Blitz markiert. Terme, die ergänzt wurden, sind rot. Die Lösung ist natürlich nicht eindeutig.