Kapitel 10: Differenzialrechnung (S. 143)
Aufgabe 1
(a) Hierzu benutzen wir die Formel für die Tangentengleichung. Es folgt \(t(x)=f'(1)\cdot (x-1)+f(1)\)
\(=(3\cdot 1^2-2)\cdot (x-1)+(1^3-2\cdot 1+1)\) \(=1\cdot (x-1)+0\) \(=x-1\)(b)
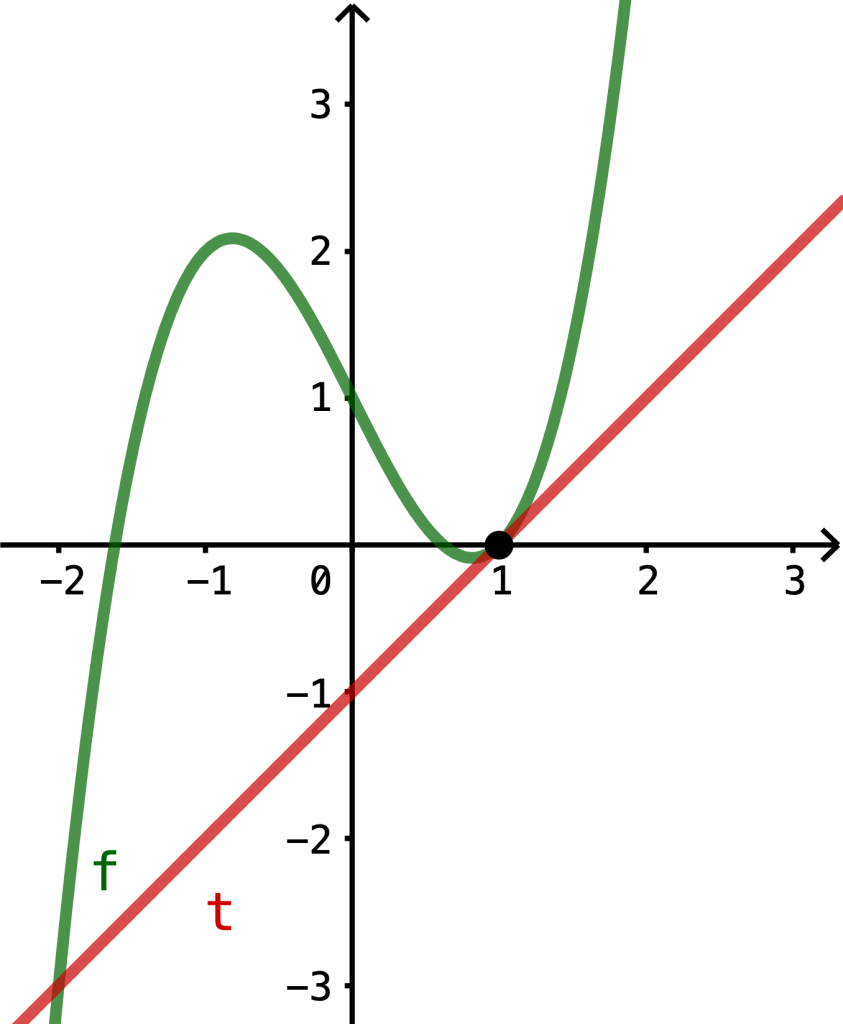
(c) Die Steigung der Tangente ist der Wert der Ableitungsfunktion an dieser Stelle. Daher hat die Tangente genau dort die Steigung 0 (ist also konstant), wenn \(f'(x_0)=0\) gilt. Mit \(3x^2-2=0\) lässt sich direkt durch Umstellen ermitteln, dass dies für \(x_0=-\sqrt{\frac{2}{3}}\approx -0,82\) oder \(x_0=\sqrt{\frac{2}{3}}\approx 0,82\) der Fall ist. Da die Tangente hier konstant (und somit parallel zur x-Achse ist), können wir direkt die Tangentengleichungen \(t(x)=-\sqrt{\frac{2}{3}}\) bzw. \(t(x)=\sqrt{\frac{2}{3}}\) für diese Fälle notieren.
(d) Wenn die Tangente fällt, hat sie negative Steigung. Wenn sie steigt, positive. Entsprechend ist die Steigung der Tangente (und somit auch der Wert der Ableitung) negativ zwischen \(-\sqrt{\frac{2}{3}}\) und \(\sqrt{\frac{2}{3}}\). Außerhalb dieses Intervalls ist sie positiv. Immer wenn der Wert der Steigung vom Positiven ins Negative oder umgekehrt wechselt, muss er zwischendurch einmal null werden.
Aufgabe 2
Da \(g(x)=3\) selbst eine konstante Funktion ist, hat die Tangente überall die Steigung 0. Entsprechendes gilt somit auch für die Ableitung, so dass einheitlich \(g'(x)=0\) gilt.