Kapitel 10: Differenzialrechnung (S. 166)

Aufgabe 1

(a) \(i'(x)=\frac{4^x\cdot\ln x\cdot \ln x – 4^x \cdot \frac{1}{x}}{4x^2}=\frac{4^x\cdot(\ln x)^2 – 4^x \cdot \frac{1}{x}}{4x^2}=\frac{4^x\cdot((\ln x)^2 – \frac{1}{x})}{4x^2}\)

(b) \(j'(x)=\sqrt{2}e^x\cos x+\sqrt{2}e^x\sin x=\sqrt{2}e^x(\cos x+\sin x)\)

Aufgabe 2

Schreibe die Funktionen als \(f(x)=x^{-1}\) bzw. \(g(x) = x^{0,5}\). Wenn du hier die Potenzregel anwendest und ggfs. wieder zurück umformst, erhältst du auch die entsprechende Ableitung. Für \(h(x)=x^{\frac{1}{n}}\) ergibt sich \(h'(x)=\frac{1}{n} x^{\frac{1}{n}-1}=\frac{1}{n} x^{\frac{1}{n}-\frac{n}{n}}=\frac{1}{n} x^{\frac{1-n}{n}}=\frac{1}{n} x^{-\frac{n-1}{n}}=\frac{1}{n}\cdot \frac{1}{x^{\frac{n-1}{n}}}=\frac{1}{n\cdot \sqrt[n]{x^{n-1}}}=\frac{\sqrt[n]{x}}{n\cdot (\sqrt[n]{x})^n}=\frac{\sqrt[n]{x}}{n\cdot x}\).

Aufgabe 3

Die Ableitung ist zunächst negativ, wird dann wieder positiv und ist dann wieder negativ. Das passt nur zu einer nach unten geöffneten Parabel. Außerdem sieht die Funktion aus wie eine Funktion dritten Grades, so dass die Ableitung entsprechend eine quadratische Funktion ist.

Aufgabe 4

(a) Es gilt \(s(30)=9 [m]\), \(s(50)=25 [m]\) und \(s(100)=100 [m]\).

(b) Die Idee ist es hier, die eigentliche Funktion durch ihre Tangente an der Stelle \(v_0=50\) zu ersetzen. Für ihre Ableitung gilt \(s'(v)=\frac{v}{50}\). Hiermit folgt \(t(v)=s'(v_0)\cdot (v-v_0) + s(v_0)=v-50+25=v-25\).

(c) Die Formel ist auf jeden Fall einfacher. Sie führt z.T. aber zu deutlich anderen Werten. Es gilt \(t(30)=5 [m]\), \(t(50)=25 [m]\) und \(t(100)=75 [m]\). Im ersten Fall macht man einen Fehler von 4 Metern, im zweiten Fall von 0 Metern und im dritten Fall von 25 Metern. In den meisten Fällen scheint die neue Formel den Bremsweg im Vergleich zur alten Formel zu unterschätzen, was natürlich gefährlich sein kann. Dass die Formel für den Wert \(v_0=50\) dasselbe Ergebnis liefert, ist nicht verwunderlich, da wir sie ja als Tangentengleichung an dieser Stelle hergeleitet haben.

Aufgabe 5

(a) Es gilt \(f(x)=(x+1)^2+0\). Der Scheitelpunkt hat daher die Koordinaten \((-1|0)\).

(b) Der Scheitelpunkt einer quadratischen Funktion ist dasselbe wie ein Hochpunkt oder Tiefpunkt. Da jede quadratische Funktion einen solchen besitzt, ist die Überprüfung mit dem hinreichenden Kriterium nicht notwendig und es reicht, das notwendige Kriterium heranzuziehen: \(f'(x)=2x+2=0\). Daraus folgt \(x=-1\) und damit die Koordinaten \((-1|0)\).

Aufgabe 6

Wenn eine Funktion wie beschrieben verschoben wird, muss nur die Verschiebung in horizontale Richtung berücksichtigt werden. Eine Verschiebung in y-Richtung verändert die Ableitung nicht. Dies kannst du dir so vorstellen, dass diese ja lediglich eine Konstante auf den Funktionsterm hinzuaddiert, die dann beim Ableiten wiederum wegfallen würde. Das neue \(f‘\) sieht also aus wie das alte lediglich um zwei Einheiten nach rechts verschoben:

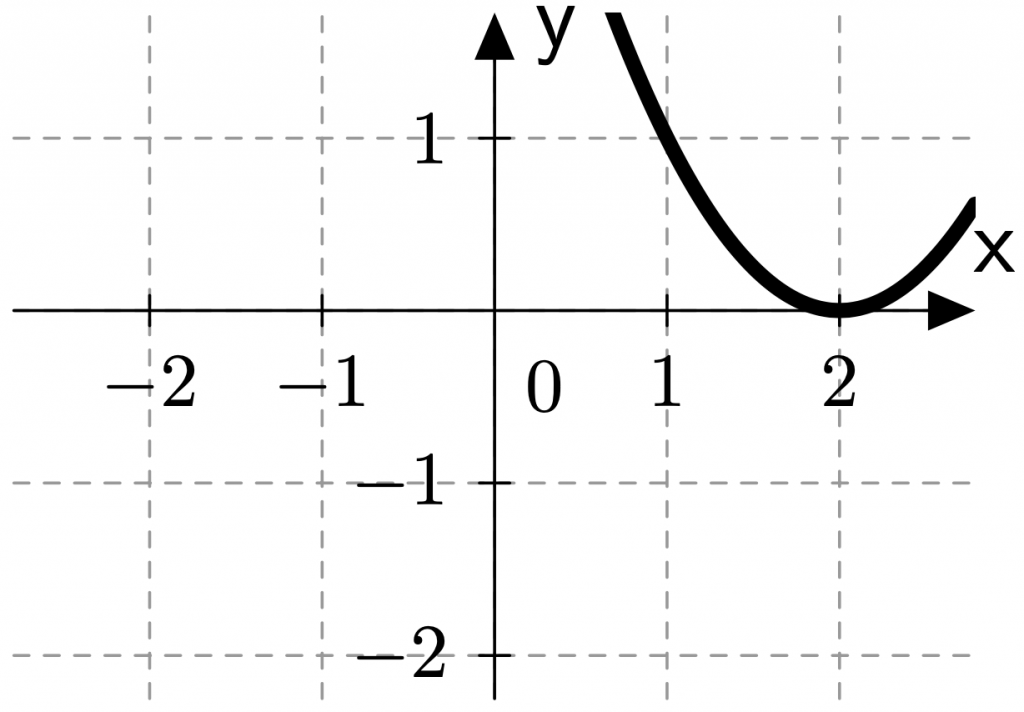
Aufgabe 7

(a) Die Lösung der Gleichung ist die eulersche Zahl \(e\), da \(\ln x\) und \(e^x\) Umkehrfunktionen zueinander sind.

(b) Aufgrund des Zusammenhangs in (a) kann man hierzu das Newton-Verfahren auf die Funktion \(f(x)=\ln x – 1\) anwenden. Hier gilt \(f'(x)=\frac{1}{x}\) und damit \(x_{n+1}=x_n-\frac{\ln x_n – 1}{\frac{1}{x_n}}=x_n-x_n\ln x_n + x_n=2x_n-x_n\ln x_n\).

Wir nutzen als Startwert eine beliebige Zahl, die bereits möglichst nah an \(e\) liegt, z.B. \(x_1=1\). Es folgt:

\(x_2=2x_1-x_1\ln x_1=2\)

\(x_3=2x_2-x_2\ln x_2=2,613705639\)

\(x_4=2x_3-x_3\ln x_3=2,716243926\)

\(x_5=2x_4-x_4\ln x_4=2,718281064\)

\(x_6=2x_5-x_5\ln x_5=2,718281828\)

Dies ist bereits der Wert, den mein Taschenrechner mit der Taste \(e\) ausgibt. Die Näherung ist also nach fünf Schritten des Newton-Verfahrens schon genau so gut, wie jene, die der Taschenrechner speichert.