Kapitel 10: Differenzialrechnung (S. 161)
Aufgabe 1
Wir haben schon eigene Informationen zusammen: Die Funktion geht gegen unendlich, egal in welche Richtung wir auf der x-Achse laufen. Außerdem wissen wir, dass sie maximal vier Nullstellen, maximal drei lokale Extremstellen und maximal zwei Wendestellen hat.
Am Term sieht man sofort, dass 0 eine Nullstelle ist. 0 ist sogar doppelte Nullstelle, da man es zweimal rausteilen kann. Du kannst nämlich \(g\) als \(g(x)=x\cdot x\cdot (x^2-3)\) schreiben. Die erste und zweite Ableitung sind schnell bestimmt, so dass man sieht, dass beide auf jeden Fall auch eine Nullstelle haben werden. Wenn die Funktion somit mindestens eine Wendestelle besitzt, muss sie beim vorliegenden Unendlichkeitsverhalten mehr als eine lokale Extremstelle haben. Hätte sie zwei lokale Extremstellen widerspräche das dem Unendlichkeitsverhalten (Versuche dir einmal einen entsprechenden Graphen vorzustellen – das geht nicht!). Also hat sie drei Extremstellen und daher auch zwei Wendestellen.
Konkret sieht ihr Graph so aus:
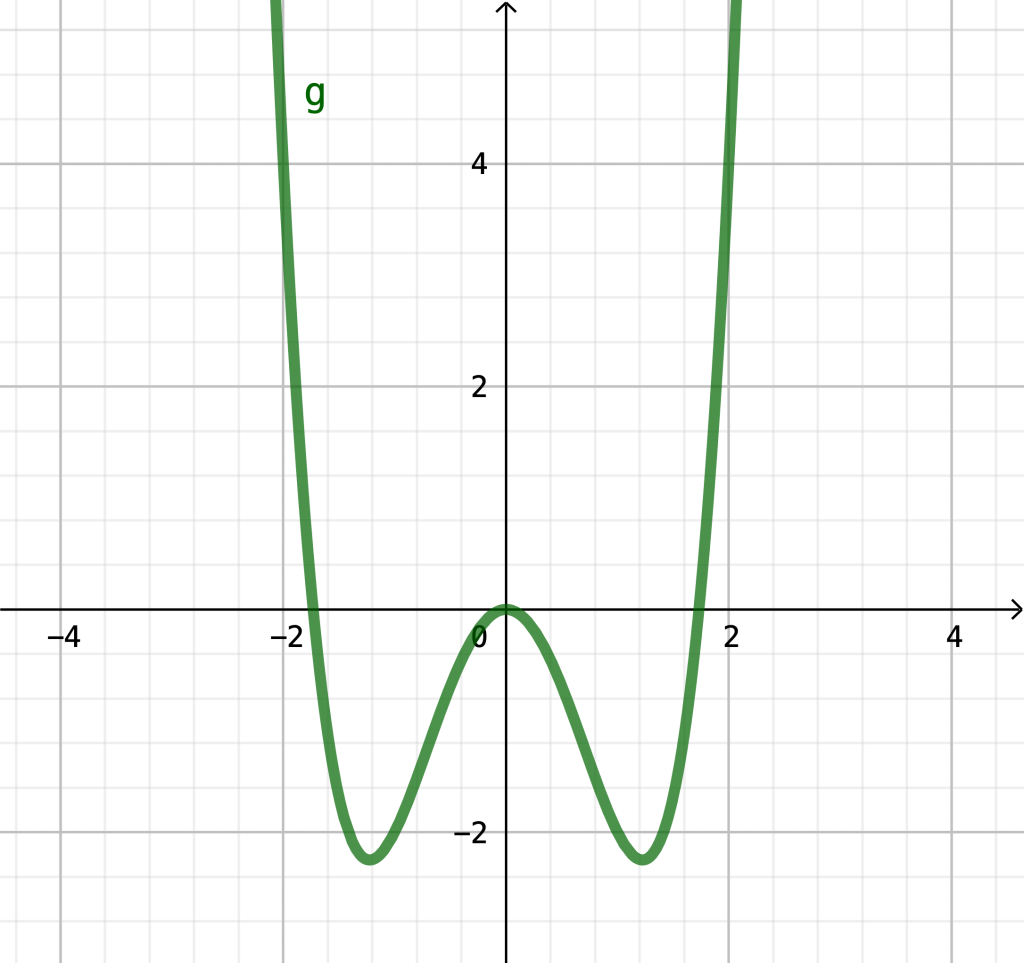
Aufgabe 2
(a) Die Funktion kann als \(f(x)=2\cdot (x^2+x-2)\) geschrieben werden. Durch Probieren (oder auch mithilfe der p-q-Formel) findet man die beiden Nullstellen des zweiten Faktors: -2 und 1. Entsprechend lässt sich die Funktion in ihrer Linearfaktorzerlegung schreiben als \(f(x)=2\cdot (x-1)\cdot (x+2)\).
Die Funktion geht gegen \(\infty\), egal in welche Richtung der x-Achse man schaut.
(b) Zunächst kann man zu \(g(x)=2x\cdot (x^2+x-4)\) umformulieren. Der letzte Faktor hat die Nullstellen \(\frac{-(\sqrt{17}+1)}{2}\) und \(\frac{\sqrt{17}-1}{2}\). Als Linearfaktorzerlegung erhalten wir entsprechend \(g(x)=2\cdot x\cdot (x-\frac{-(\sqrt{17}+1)}{2})\cdot (x-\frac{\sqrt{17}-1}{2})\).
Die Funktion geht gegen \(-\infty\) für \(x\) gegen \(-\infty\) und gegen \(\infty\) für \(x\) gegen \(\infty\)
(c) Wenn man den Graph der Funktion erstellt, sieht man, dass sie nur eine Nullstelle hat. Sie besitzt damit keine Linearfaktorzerlegung wie im Satz auf S. 160 beschrieben. Alternativ kann man die Nullstelle -1 erraten und versuchen die Funktion in die Form \(h(x)=(x+1)\cdot\ldots\) zu bringen und erhält mit etwas Knobeln \(h(x)=(x+1)\cdot(x^2+2)\). Der zweite Faktor hat allerdings keine Nullstellen, so dass dann auch auf diesem Weg Schluss ist und eine Linearfaktorzerlegung nicht möglich ist.
Die Funktion geht auch gegen \(-\infty\) für \(x\) gegen \(-\infty\) und gegen \(\infty\) für \(x\) gegen \(\infty\)
Aufgabe 3
Hierzu schreibt man die zweite Ableitung direkt als Linearfaktorzerlegung mit den gewünschten Nullstellen auf, z.B. indem man \(f^{\prime\prime}(x)=x(x-1)=x^2-x\) setzt. Die Nullstellen sind dann wie gewünscht \(x=0\) und \(x=1\). Die dritten Ableitung ist \(f^{\prime\prime\prime}(x)=2x-1\), was für beide Werte ungleich null ist. Die erste Ableitung ist dann \(f'(x)=\frac{1}{3}x^3-\frac{1}{2}x^2\) und die Funktion selbst \(f(x)=\frac{1}{12}x^4-\frac{1}{6}x^3\).
Kommt dir bekannt vor? Hierbei handelt es sich übrigens um dieselbe Lösung wie auf S. 155, Aufgabe 2 (b).